
 Read Online or Download
Table of Contents, Index
Lecture Notes
Special Relativity Practice Problems
Sometimes it is more convenient to talk about distances in
terms of light-time. For example:
It takes light one nanosecond to propagate one foot.
The distance to the Moon is about 1.3 light-seconds.
The distance to the Sun is about 8.3 light-minutes.
We see the Sun as it was 8.3 minutes ago.
The Voyager 1 spacecraft, out beyond the Kuiper Belt, is more
that 19.6 light-hours away.
The closest star, Proxima Centauri, is 4.24 light-years away.
The brightest star, Sirius, is 8.6 light-years away. Seriously!
There is a fuzzy smudge of light visible to human eyes on a
dark night, M31, the Andromeda Galaxy--it is 2.5 million
light-years away. We can't see the Andromeda Galaxy as it is
"now". We can only see it as it was 2.5 million years ago.
At dinner, I like to point out to my guests at the other end
of the 10 foot table that I do not see them as the are "now",
but as they were 10ns ago.
Looking out in space is the equivalent to back in time--at
the dining room table and across the universe.
Read Online or Download
Table of Contents, Index
Lecture Notes
Special Relativity Practice Problems
Sometimes it is more convenient to talk about distances in
terms of light-time. For example:
It takes light one nanosecond to propagate one foot.
The distance to the Moon is about 1.3 light-seconds.
The distance to the Sun is about 8.3 light-minutes.
We see the Sun as it was 8.3 minutes ago.
The Voyager 1 spacecraft, out beyond the Kuiper Belt, is more
that 19.6 light-hours away.
The closest star, Proxima Centauri, is 4.24 light-years away.
The brightest star, Sirius, is 8.6 light-years away. Seriously!
There is a fuzzy smudge of light visible to human eyes on a
dark night, M31, the Andromeda Galaxy--it is 2.5 million
light-years away. We can't see the Andromeda Galaxy as it is
"now". We can only see it as it was 2.5 million years ago.
At dinner, I like to point out to my guests at the other end
of the 10 foot table that I do not see them as the are "now",
but as they were 10ns ago.
Looking out in space is the equivalent to back in time--at
the dining room table and across the universe.

 Street Lamps Problem
http://www1.phys.vt.edu/~takeuchi/relativity/practice/problem02.html
Street Lamps Problem
http://www1.phys.vt.edu/~takeuchi/relativity/practice/problem02.html
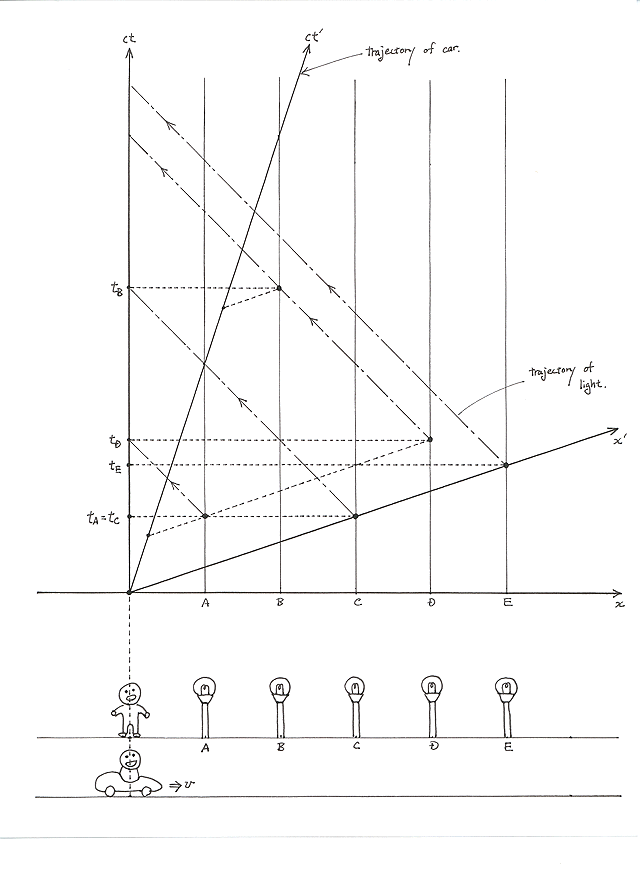 Five street lamps A, B, C, D, and E are located on a
straight line along the x axis equal distance apart as shown
in the figure. They turn on at times tA, tB, tC, tD, and tE,
respectively, in the frame at rest relative to the ground.
This is indicated in the space-time diagram above the
figure.
What is the order in which the lamps turn on in this frame?
A and C simultaneously, then E, then D, and then B.
What is the order in which the light of the lamps reach the
observer at x=0?
A, then C, then B and D simultaneously, and then E.
A car is moving at constant velocity relative to the ground.
At t'=t=0, it is at x'=x=0. The space and time axes in the
moving frame of the car are tilted with respect to those of
the rest frame as shown in the space-time diagram. What is
the order in which the lamps turn on in this frame?
C and E simultaneously, then A and D simultaneously, and then B.
What is the order in which the light from the lamps reach
the observer riding the car?
A, then C, then B and D simultaneously, and then E.
Where is the car when the light from street lamp D reaches
it?
Between street lamps A and B.
Space-Time Diagram from Wolfram Alpha
https://demonstrations.wolfram.com/SpacetimeDiagram/
Space-Time Diagram from GeoGebra
https://www.geogebra.org/m/BRSSmQZH
Interactive Minkowski Diagram
https://sciencesims.com/sims/minkowski/
Lorentz Factor Calculator 𝛾 = 1/√(1-(v^2/c^2))
https://www.azcalculator.com/calc/lorentz-factor-calculator.php
https://en.wikipedia.org/wiki/Lorentz_factor
Five street lamps A, B, C, D, and E are located on a
straight line along the x axis equal distance apart as shown
in the figure. They turn on at times tA, tB, tC, tD, and tE,
respectively, in the frame at rest relative to the ground.
This is indicated in the space-time diagram above the
figure.
What is the order in which the lamps turn on in this frame?
A and C simultaneously, then E, then D, and then B.
What is the order in which the light of the lamps reach the
observer at x=0?
A, then C, then B and D simultaneously, and then E.
A car is moving at constant velocity relative to the ground.
At t'=t=0, it is at x'=x=0. The space and time axes in the
moving frame of the car are tilted with respect to those of
the rest frame as shown in the space-time diagram. What is
the order in which the lamps turn on in this frame?
C and E simultaneously, then A and D simultaneously, and then B.
What is the order in which the light from the lamps reach
the observer riding the car?
A, then C, then B and D simultaneously, and then E.
Where is the car when the light from street lamp D reaches
it?
Between street lamps A and B.
Space-Time Diagram from Wolfram Alpha
https://demonstrations.wolfram.com/SpacetimeDiagram/
Space-Time Diagram from GeoGebra
https://www.geogebra.org/m/BRSSmQZH
Interactive Minkowski Diagram
https://sciencesims.com/sims/minkowski/
Lorentz Factor Calculator 𝛾 = 1/√(1-(v^2/c^2))
https://www.azcalculator.com/calc/lorentz-factor-calculator.php
https://en.wikipedia.org/wiki/Lorentz_factor
 Five Papers That Shook the World
https://physicsworld.com/a/five-papers-that-shook-the-world/
ON THE ELECTRODYNAMICS OF MOVING BODIES By A. Einstein
http://www.fourmilab.ch/etexts/einstein/specrel/specrel.pdf
Beautiful, Simple and Profound (90 min)
https://www.youtube.com/watch?v=R_yk45m4E3M
https://www.youtube.com/watch?v=ASzECGtSpqQ
Spacetime: All the universe's a stage
https://www.symmetrymagazine.org/article/spacetime-all-the-universes-a-stage
Feynman Diagrams
https://www.youtube.com/watch?v=qe7atm1x6Mg
sam.wormley@icloud.com
Five Papers That Shook the World
https://physicsworld.com/a/five-papers-that-shook-the-world/
ON THE ELECTRODYNAMICS OF MOVING BODIES By A. Einstein
http://www.fourmilab.ch/etexts/einstein/specrel/specrel.pdf
Beautiful, Simple and Profound (90 min)
https://www.youtube.com/watch?v=R_yk45m4E3M
https://www.youtube.com/watch?v=ASzECGtSpqQ
Spacetime: All the universe's a stage
https://www.symmetrymagazine.org/article/spacetime-all-the-universes-a-stage
Feynman Diagrams
https://www.youtube.com/watch?v=qe7atm1x6Mg
sam.wormley@icloud.com
Read Online or Download Table of Contents, Index Lecture Notes Special Relativity Practice Problems Sometimes it is more convenient to talk about distances in terms of light-time. For example: It takes light one nanosecond to propagate one foot. The distance to the Moon is about 1.3 light-seconds. The distance to the Sun is about 8.3 light-minutes. We see the Sun as it was 8.3 minutes ago. The Voyager 1 spacecraft, out beyond the Kuiper Belt, is more that 19.6 light-hours away. The closest star, Proxima Centauri, is 4.24 light-years away. The brightest star, Sirius, is 8.6 light-years away. Seriously! There is a fuzzy smudge of light visible to human eyes on a dark night, M31, the Andromeda Galaxy--it is 2.5 million light-years away. We can't see the Andromeda Galaxy as it is "now". We can only see it as it was 2.5 million years ago. At dinner, I like to point out to my guests at the other end of the 10 foot table that I do not see them as the are "now", but as they were 10ns ago. Looking out in space is the equivalent to back in time--at the dining room table and across the universe.

Street Lamps Problem http://www1.phys.vt.edu/~takeuchi/relativity/practice/problem02.html
Five street lamps A, B, C, D, and E are located on a straight line along the x axis equal distance apart as shown in the figure. They turn on at times tA, tB, tC, tD, and tE, respectively, in the frame at rest relative to the ground. This is indicated in the space-time diagram above the figure. What is the order in which the lamps turn on in this frame? A and C simultaneously, then E, then D, and then B. What is the order in which the light of the lamps reach the observer at x=0? A, then C, then B and D simultaneously, and then E. A car is moving at constant velocity relative to the ground. At t'=t=0, it is at x'=x=0. The space and time axes in the moving frame of the car are tilted with respect to those of the rest frame as shown in the space-time diagram. What is the order in which the lamps turn on in this frame? C and E simultaneously, then A and D simultaneously, and then B. What is the order in which the light from the lamps reach the observer riding the car? A, then C, then B and D simultaneously, and then E. Where is the car when the light from street lamp D reaches it? Between street lamps A and B. Space-Time Diagram from Wolfram Alpha https://demonstrations.wolfram.com/SpacetimeDiagram/ Space-Time Diagram from GeoGebra https://www.geogebra.org/m/BRSSmQZH Interactive Minkowski Diagram https://sciencesims.com/sims/minkowski/ Lorentz Factor Calculator 𝛾 = 1/√(1-(v^2/c^2)) https://www.azcalculator.com/calc/lorentz-factor-calculator.php https://en.wikipedia.org/wiki/Lorentz_factor
Five Papers That Shook the World https://physicsworld.com/a/five-papers-that-shook-the-world/ ON THE ELECTRODYNAMICS OF MOVING BODIES By A. Einstein http://www.fourmilab.ch/etexts/einstein/specrel/specrel.pdf Beautiful, Simple and Profound (90 min) https://www.youtube.com/watch?v=R_yk45m4E3M https://www.youtube.com/watch?v=ASzECGtSpqQ Spacetime: All the universe's a stage https://www.symmetrymagazine.org/article/spacetime-all-the-universes-a-stage Feynman Diagrams https://www.youtube.com/watch?v=qe7atm1x6Mg sam.wormley@icloud.com
