My Fridays with Dave Martin
Physicists Just Discovered The Ultimate 'Kings And Queens' of
Quantumness
https://www.sciencealert.com/physicists-just-discovered-the-ultimate-kings-and-queens-of-quantumness
What Effects Of Quantum Physics Can We Observe In Our Daily
Lives? Everything except gravity. What?
https://www.forbes.com/sites/quora/2017/01/20/what-effects-of-quantum-physics-can-we-observe-in-our-daily-lives/#13c841ad7725
In a trivial sense, everything you see around you is a
quantum phenomenon because it's made of elementary particles
that are described by quantum mechanics. It so happens that
quantum mechanics reproduces classical physics in the
appropriate limits, but they're all fundamentally quantum. A
basketball bouncing is a quantum effect because it's made up
of molecules all obeying quantum rules, and all those
molecules just happen to add up to a basketball. That's
probably not what you wanted to hear, though.
In a slightly stronger sense, classical physics is an
inadequate way to describe much of anything at a fundamental
level. Say you're a classical physicist and you want to
build a bridge. You'll be able to do it because you can use
the stress-strain relationship of your steel girders to
model the deformation of the bridge under its load, and you
can work it all out with a bunch of math and computer
models. But where does this stress-strain relationship come
from? A classical physicist has no idea. If you want to know
why your steel has the properties it does, you need to know
the energy change as you change its shape, but that energy
is stored in electrons orbiting nuclei, so it's quantum
mechanical. Indeed, you can estimate the Young's modulus of
steel from fundamental things like the electron charge,
etc., but you will need to include Planck's constant in that
calculation. That's not special to steel girders - there's
no classical theory of why matter works out the way it does.
Classical atoms should decay. Without quantum mechanics,
there's no matter at all.
 Wikipedia -- Pauli exclusion principle
https://en.wikipedia.org/wiki/Pauli_exclusion_principle
The Pauli exclusion principle is the quantum mechanical
principle which states that two or more identical fermions
(particles with half-integer spin) cannot occupy the same
quantum state within a quantum system simultaneously. In the
case of electrons in atoms, it can be stated as follows: it
is impossible for two electrons of a poly-electron atom to
have the same values of the four quantum numbers: n, the
principal quantum number, l, the angular momentum quantum
number, ml, the magnetic quantum number, and ms, the spin
quantum number. For example, if two electrons reside in the
same orbital, and if their n, l, and ml values are the same,
then their ms must be different, and thus the electrons must
have opposite half-integer spin projections of 1/2 and -1/2.
This principle was formulated by Austrian physicist Wolfgang
Pauli in 1925 for electrons, and later extended to all
fermions with his spin-statistics theorem of 1940.
In one sense, it's hard not to see quantum mechanics in
everyday life. For example, the existence of complex
chemistry and the volume occupied by ordinary matter are
both direct consequences of the Pauli exclusion principle.
Energy Level Within Atomic Structure
Wikipedia -- Pauli exclusion principle
https://en.wikipedia.org/wiki/Pauli_exclusion_principle
The Pauli exclusion principle is the quantum mechanical
principle which states that two or more identical fermions
(particles with half-integer spin) cannot occupy the same
quantum state within a quantum system simultaneously. In the
case of electrons in atoms, it can be stated as follows: it
is impossible for two electrons of a poly-electron atom to
have the same values of the four quantum numbers: n, the
principal quantum number, l, the angular momentum quantum
number, ml, the magnetic quantum number, and ms, the spin
quantum number. For example, if two electrons reside in the
same orbital, and if their n, l, and ml values are the same,
then their ms must be different, and thus the electrons must
have opposite half-integer spin projections of 1/2 and -1/2.
This principle was formulated by Austrian physicist Wolfgang
Pauli in 1925 for electrons, and later extended to all
fermions with his spin-statistics theorem of 1940.
In one sense, it's hard not to see quantum mechanics in
everyday life. For example, the existence of complex
chemistry and the volume occupied by ordinary matter are
both direct consequences of the Pauli exclusion principle.
Energy Level Within Atomic Structure
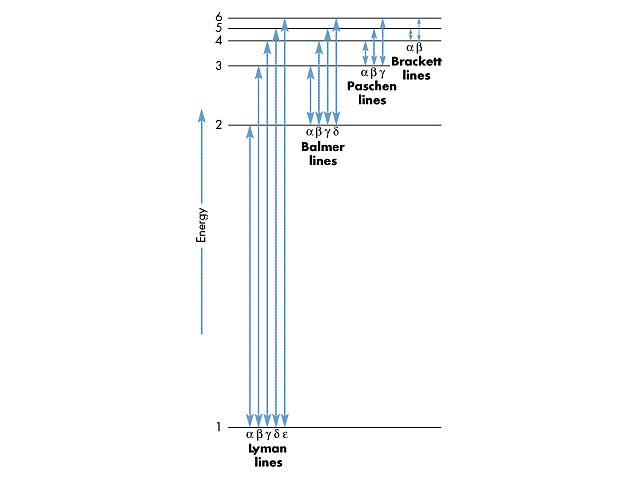 Wikipedia -- Emission spectrum
https://en.wikipedia.org/wiki/Emission_spectrum
The emission spectrum of a chemical element or chemical
compound is the spectrum of frequencies of electromagnetic
radiation emitted due to an atom or molecule making a
transition from a high energy state to a lower energy state.
The photon energy of the emitted photon is equal to the
energy difference between the two states.
Wikipedia -- Emission spectrum
https://en.wikipedia.org/wiki/Emission_spectrum
The emission spectrum of a chemical element or chemical
compound is the spectrum of frequencies of electromagnetic
radiation emitted due to an atom or molecule making a
transition from a high energy state to a lower energy state.
The photon energy of the emitted photon is equal to the
energy difference between the two states.
 Use a prism (or a diffraction grating if you have one) to
break up the light coming from a florescent bulb. You'll see
a bunch of individual lines rather than a continuous band of
colors. This comes from the discrete energy levels in atoms
and molecules, which is a consequence of quantum mechanics.
Quantum mechanics and everyday nature
Reflections on Everyday Quantum Events
https://www.quora.com/How-do-mirrors-work-on-a-quantum-level?share=1
https://physics.stackexchange.com/questions/65397/quantum-mechanics-and-everyday-nature
Mirror
A roaming electron does not sound all that unusual until you
realize that electrons are so very light that quantum
mechanics cannot be ignored. What quantum mechanics does to
very light objects is cause their quantum descriptions to
start taking up space across the entire volume of the metal
over which they roam. That is, instead of an electron moving
back and for the across a crystal as an massive classical
object would, an undisturbed and freely roaming electron is
most accurately represented as being equally located at all
locations in the metal at the same time.
The quantum magic begins whenever you look into an ordinary
mirror. As soon as you do, you are already gazing into a sea
of electrons that from a quantum mechanical perspective
don't quite exist in ordinary space. They are "lost" in the
XYZ space we know best, a space in which their accurate
quantum representations are in some cases as large as the
entire surface of the mirror.
And most of those lost electrons are also hidden! That's
because light that we see bouncing off a mirror comes from
only a very tiny percentage of the Fermi sea electrons,
specifically only the extremely hot ones at the very top of
the Fermi sea. This is because they are the only electrons
that have any "wiggle room" left to accept a photon and play
catch with it.
What happens is this: An electron at the Fermi sea surface
can accept a particle of light, a photon, and by doing so
speed itself up just a little more. But unlike the electrons
further down in the sea, when an electron at the surface
speeds up it creates an "empty spot" in the Fermi sea. The
process is closely akin to the ways a splash of water can
rise up into air, but then realizes it no longer has any
water below it to keep it supported. Unlike the water in the
see, the splash above the surface is not stable: It has to
fall back to the surface.
Very much like such a splash of water, an electron at the
Fermi surface that has been "splashed up" by an incoming
particle of light (photon) has no support underneath it to
keep it there. So, it must fall back to the surface of the
Fermi sea. As it does so, it gives up the photon energy that
it held ever so briefly by re-emitting a nearly identical
version of the photon it just absorbed. This re-emission of
a photon from an electron at the Fermi surface is the
smallest and most fundamental unit of reflection, the event
from which larger_scale reflections are composed.
Heisenberg's Uncertainty Principle Explained (4+ min)
https://www.youtube.com/watch?v=a8FTr2qMutA
Use a prism (or a diffraction grating if you have one) to
break up the light coming from a florescent bulb. You'll see
a bunch of individual lines rather than a continuous band of
colors. This comes from the discrete energy levels in atoms
and molecules, which is a consequence of quantum mechanics.
Quantum mechanics and everyday nature
Reflections on Everyday Quantum Events
https://www.quora.com/How-do-mirrors-work-on-a-quantum-level?share=1
https://physics.stackexchange.com/questions/65397/quantum-mechanics-and-everyday-nature
Mirror
A roaming electron does not sound all that unusual until you
realize that electrons are so very light that quantum
mechanics cannot be ignored. What quantum mechanics does to
very light objects is cause their quantum descriptions to
start taking up space across the entire volume of the metal
over which they roam. That is, instead of an electron moving
back and for the across a crystal as an massive classical
object would, an undisturbed and freely roaming electron is
most accurately represented as being equally located at all
locations in the metal at the same time.
The quantum magic begins whenever you look into an ordinary
mirror. As soon as you do, you are already gazing into a sea
of electrons that from a quantum mechanical perspective
don't quite exist in ordinary space. They are "lost" in the
XYZ space we know best, a space in which their accurate
quantum representations are in some cases as large as the
entire surface of the mirror.
And most of those lost electrons are also hidden! That's
because light that we see bouncing off a mirror comes from
only a very tiny percentage of the Fermi sea electrons,
specifically only the extremely hot ones at the very top of
the Fermi sea. This is because they are the only electrons
that have any "wiggle room" left to accept a photon and play
catch with it.
What happens is this: An electron at the Fermi sea surface
can accept a particle of light, a photon, and by doing so
speed itself up just a little more. But unlike the electrons
further down in the sea, when an electron at the surface
speeds up it creates an "empty spot" in the Fermi sea. The
process is closely akin to the ways a splash of water can
rise up into air, but then realizes it no longer has any
water below it to keep it supported. Unlike the water in the
see, the splash above the surface is not stable: It has to
fall back to the surface.
Very much like such a splash of water, an electron at the
Fermi surface that has been "splashed up" by an incoming
particle of light (photon) has no support underneath it to
keep it there. So, it must fall back to the surface of the
Fermi sea. As it does so, it gives up the photon energy that
it held ever so briefly by re-emitting a nearly identical
version of the photon it just absorbed. This re-emission of
a photon from an electron at the Fermi surface is the
smallest and most fundamental unit of reflection, the event
from which larger_scale reflections are composed.
Heisenberg's Uncertainty Principle Explained (4+ min)
https://www.youtube.com/watch?v=a8FTr2qMutA
 Quantum effects observed in photosynthesis
https://phys.org/news/2014-01-quantum-mechanics-efficiency-photosynthesis.html
https://www.youtube.com/watch?v=_RSKI5A_lsg (4+ min)
Wikipedia -- Quantum Tunneling
https://en.wikipedia.org/wiki/Tunnel_diode
https://en.wikipedia.org/wiki/Quantum_tunnelling
Quantum tunneling is the quantum mechanical phenomenon where
a particle passes through a potential barrier that it
classically cannot surmount. This plays an essential role in
several physical phenomena, such as the nuclear fusion that
occurs in main sequence stars like the Sun. It has important
applications to modern devices such as the tunnel diode,
quantum computing, and the scanning tunnelling microscope.
The effect was predicted in the early 20th century, and its
acceptance as a general physical phenomenon came
mid-century.
Fundamental quantum mechanical concepts are central to this
phenomenon, which makes quantum tunneling one of the novel
implications of quantum mechanics. Quantum tunneling is
projected to create physical limits to how small transistors
can get, due to electrons being able to tunnel past them if
they are too small.
Tunneling is often explained in terms of the Heisenberg
uncertainty principle and the premise that the quantum
object has more than one fixed state (not a wave nor a
particle) in general.
Liquid helium-3 and helium-4 are remarkable substances.
https://physicstoday.scitation.org/doi/full/10.1063/PT.3.4067
Liquid helium-3 and helium-4 are remarkable substances. They
are quantum liquids, meaning that their behavior is governed
by the laws of quantum mechanics. Because of their small
atomic mass, each isotope exists in a liquid state down to
the temperature of absolute zero. And at sufficiently low
temperature, each becomes a superfluid. However, the two
isotopes have very different properties because 3He is a
fermion and 4He is a boson. As a result of their different
statistics, superfluidity in 3He appears at a temperature
one-thousandth of that at which superfluid 4He forms. A
second difference is that 3He has multiple thermodynamic
phases.
The quest to test quantum entanglement
https://www.symmetrymagazine.org/article/the-quest-to-test-quantum-entanglement
sam.wormley@icloud.com
Quantum effects observed in photosynthesis
https://phys.org/news/2014-01-quantum-mechanics-efficiency-photosynthesis.html
https://www.youtube.com/watch?v=_RSKI5A_lsg (4+ min)
Wikipedia -- Quantum Tunneling
https://en.wikipedia.org/wiki/Tunnel_diode
https://en.wikipedia.org/wiki/Quantum_tunnelling
Quantum tunneling is the quantum mechanical phenomenon where
a particle passes through a potential barrier that it
classically cannot surmount. This plays an essential role in
several physical phenomena, such as the nuclear fusion that
occurs in main sequence stars like the Sun. It has important
applications to modern devices such as the tunnel diode,
quantum computing, and the scanning tunnelling microscope.
The effect was predicted in the early 20th century, and its
acceptance as a general physical phenomenon came
mid-century.
Fundamental quantum mechanical concepts are central to this
phenomenon, which makes quantum tunneling one of the novel
implications of quantum mechanics. Quantum tunneling is
projected to create physical limits to how small transistors
can get, due to electrons being able to tunnel past them if
they are too small.
Tunneling is often explained in terms of the Heisenberg
uncertainty principle and the premise that the quantum
object has more than one fixed state (not a wave nor a
particle) in general.
Liquid helium-3 and helium-4 are remarkable substances.
https://physicstoday.scitation.org/doi/full/10.1063/PT.3.4067
Liquid helium-3 and helium-4 are remarkable substances. They
are quantum liquids, meaning that their behavior is governed
by the laws of quantum mechanics. Because of their small
atomic mass, each isotope exists in a liquid state down to
the temperature of absolute zero. And at sufficiently low
temperature, each becomes a superfluid. However, the two
isotopes have very different properties because 3He is a
fermion and 4He is a boson. As a result of their different
statistics, superfluidity in 3He appears at a temperature
one-thousandth of that at which superfluid 4He forms. A
second difference is that 3He has multiple thermodynamic
phases.
The quest to test quantum entanglement
https://www.symmetrymagazine.org/article/the-quest-to-test-quantum-entanglement
sam.wormley@icloud.com
Wikipedia -- Pauli exclusion principle https://en.wikipedia.org/wiki/Pauli_exclusion_principle The Pauli exclusion principle is the quantum mechanical principle which states that two or more identical fermions (particles with half-integer spin) cannot occupy the same quantum state within a quantum system simultaneously. In the case of electrons in atoms, it can be stated as follows: it is impossible for two electrons of a poly-electron atom to have the same values of the four quantum numbers: n, the principal quantum number, l, the angular momentum quantum number, ml, the magnetic quantum number, and ms, the spin quantum number. For example, if two electrons reside in the same orbital, and if their n, l, and ml values are the same, then their ms must be different, and thus the electrons must have opposite half-integer spin projections of 1/2 and -1/2. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin-statistics theorem of 1940. In one sense, it's hard not to see quantum mechanics in everyday life. For example, the existence of complex chemistry and the volume occupied by ordinary matter are both direct consequences of the Pauli exclusion principle. Energy Level Within Atomic Structure
Wikipedia -- Emission spectrum https://en.wikipedia.org/wiki/Emission_spectrum The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted due to an atom or molecule making a transition from a high energy state to a lower energy state. The photon energy of the emitted photon is equal to the energy difference between the two states.
Use a prism (or a diffraction grating if you have one) to break up the light coming from a florescent bulb. You'll see a bunch of individual lines rather than a continuous band of colors. This comes from the discrete energy levels in atoms and molecules, which is a consequence of quantum mechanics. Quantum mechanics and everyday nature Reflections on Everyday Quantum Events https://www.quora.com/How-do-mirrors-work-on-a-quantum-level?share=1 https://physics.stackexchange.com/questions/65397/quantum-mechanics-and-everyday-nature Mirror A roaming electron does not sound all that unusual until you realize that electrons are so very light that quantum mechanics cannot be ignored. What quantum mechanics does to very light objects is cause their quantum descriptions to start taking up space across the entire volume of the metal over which they roam. That is, instead of an electron moving back and for the across a crystal as an massive classical object would, an undisturbed and freely roaming electron is most accurately represented as being equally located at all locations in the metal at the same time. The quantum magic begins whenever you look into an ordinary mirror. As soon as you do, you are already gazing into a sea of electrons that from a quantum mechanical perspective don't quite exist in ordinary space. They are "lost" in the XYZ space we know best, a space in which their accurate quantum representations are in some cases as large as the entire surface of the mirror. And most of those lost electrons are also hidden! That's because light that we see bouncing off a mirror comes from only a very tiny percentage of the Fermi sea electrons, specifically only the extremely hot ones at the very top of the Fermi sea. This is because they are the only electrons that have any "wiggle room" left to accept a photon and play catch with it. What happens is this: An electron at the Fermi sea surface can accept a particle of light, a photon, and by doing so speed itself up just a little more. But unlike the electrons further down in the sea, when an electron at the surface speeds up it creates an "empty spot" in the Fermi sea. The process is closely akin to the ways a splash of water can rise up into air, but then realizes it no longer has any water below it to keep it supported. Unlike the water in the see, the splash above the surface is not stable: It has to fall back to the surface. Very much like such a splash of water, an electron at the Fermi surface that has been "splashed up" by an incoming particle of light (photon) has no support underneath it to keep it there. So, it must fall back to the surface of the Fermi sea. As it does so, it gives up the photon energy that it held ever so briefly by re-emitting a nearly identical version of the photon it just absorbed. This re-emission of a photon from an electron at the Fermi surface is the smallest and most fundamental unit of reflection, the event from which larger_scale reflections are composed. Heisenberg's Uncertainty Principle Explained (4+ min) https://www.youtube.com/watch?v=a8FTr2qMutA
Quantum effects observed in photosynthesis https://phys.org/news/2014-01-quantum-mechanics-efficiency-photosynthesis.html https://www.youtube.com/watch?v=_RSKI5A_lsg (4+ min) Wikipedia -- Quantum Tunneling https://en.wikipedia.org/wiki/Tunnel_diode https://en.wikipedia.org/wiki/Quantum_tunnelling Quantum tunneling is the quantum mechanical phenomenon where a particle passes through a potential barrier that it classically cannot surmount. This plays an essential role in several physical phenomena, such as the nuclear fusion that occurs in main sequence stars like the Sun. It has important applications to modern devices such as the tunnel diode, quantum computing, and the scanning tunnelling microscope. The effect was predicted in the early 20th century, and its acceptance as a general physical phenomenon came mid-century. Fundamental quantum mechanical concepts are central to this phenomenon, which makes quantum tunneling one of the novel implications of quantum mechanics. Quantum tunneling is projected to create physical limits to how small transistors can get, due to electrons being able to tunnel past them if they are too small. Tunneling is often explained in terms of the Heisenberg uncertainty principle and the premise that the quantum object has more than one fixed state (not a wave nor a particle) in general. Liquid helium-3 and helium-4 are remarkable substances. https://physicstoday.scitation.org/doi/full/10.1063/PT.3.4067 Liquid helium-3 and helium-4 are remarkable substances. They are quantum liquids, meaning that their behavior is governed by the laws of quantum mechanics. Because of their small atomic mass, each isotope exists in a liquid state down to the temperature of absolute zero. And at sufficiently low temperature, each becomes a superfluid. However, the two isotopes have very different properties because 3He is a fermion and 4He is a boson. As a result of their different statistics, superfluidity in 3He appears at a temperature one-thousandth of that at which superfluid 4He forms. A second difference is that 3He has multiple thermodynamic phases. The quest to test quantum entanglement https://www.symmetrymagazine.org/article/the-quest-to-test-quantum-entanglement sam.wormley@icloud.com