MCC PHS 142 M01 Astronomy Homework Ch.4-5
Adj Prof Astronomy: Sam Wormley <sam.wormley@gmail.com>
Web: http://edu-observatory.org/eo/mcc.html
Background Material
Textbook - Read Chapters 4-5
Textbook - http://highered.mcgraw-hill.com/sites/0073512184/student_view0/chapter4/
Textbook - http://highered.mcgraw-hill.com/sites/0073512184/student_view0/chapter5/
(take the Multiple Choice Quiz for for each chapter)
Textbook - Glossary, pg G-1, Words like: Azimuth, Meridian, Zenith, etc.
Web - http://edu-observatory.org/eo/eclipses.html
Web - http://mathworld.wolfram.com/Ellipse.html
Web - http://mathworld.wolfram.com/Eccentricity.html
Web - http://scienceworld.wolfram.com/physics/KeplersLaws.html
Web - http://scienceworld.wolfram.com/physics/Gravity.html
Web - http://scienceworld.wolfram.com/physics/NewtonsLaws.html
Web - http://antwrp.gsfc.nasa.gov/apod/archivepix.html
 Apparent Motions of the Sky (cont.)
The Earth rotates about its polar axis once a day and produces an
apparent motion on the night sky about the celestial poles. In the
Northern Hemisphere the north celestial pole is elevated above the
horizon. Facing away from the elevated celestial pole, an observer sees
the Sun, Moon, planets, and stars rise in the east and set in the west.
They reach their highest altitude as they cross the local meridian.
When the observer turns to face the elevated celestial pole, stars
nearest the pole neither rise nor set. They become circumpolar and
cross the meridian each day once above the pole at their highest
altitude and once below the pole at their lowest altitude. In the
Northern Hemisphere, circumpolar stars appear to rotate about the north
celestial pole counterclockwise. In the Southern Hemisphere the effect
is reversed and they appear to rotate clockwise.
Superimposed on the diurnal rotation is an annual rotation caused by
the Earth's orbiting the Sun. Since the stars are seen by the naked eye
after sunset, the constellations appear to move from east to west, and
to return to the same position after a year. Relative to the Sun, the
stars rise and set roughly four minutes earlier each day. In the course
of a month, the night sky appears to move two hours in right ascension
to the west. Also because of this orbital motion of the Earth, the
circumpolar stars in the Northern Hemisphere appear to rotate once a
year in a counterclockwise direction around the north celestial pole
and in a clockwise direction about the south celestial pole.
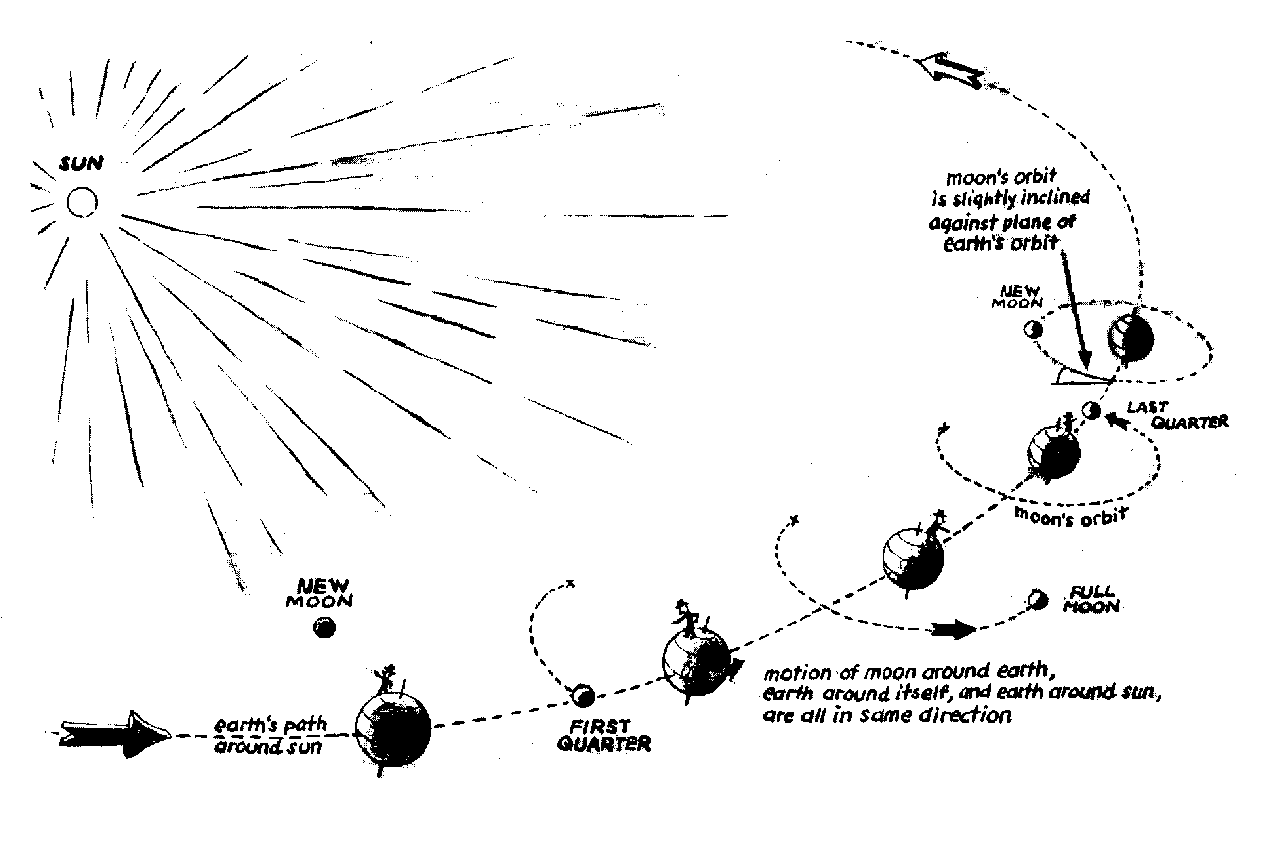
The Moon moves in an orbit inclined to the ecliptic by 5+ degrees; the
Moon makes one revolution about the sky from west to east in about a
month. During this period the phases on the Moon complete a cycle from
new to full and back to new. The orbit of the Moon is moving around the
ecliptic, so that other aspects of the Moon's position in the sky, such
as its maximum and minimum declination, change from one month the next.
The Sun, Moon and the Earth occasionally line up creating the phenomena
we call eclipses. Below is a graphic summary of eclipses for several
years.
Apparent Motions of the Sky (cont.)
The Earth rotates about its polar axis once a day and produces an
apparent motion on the night sky about the celestial poles. In the
Northern Hemisphere the north celestial pole is elevated above the
horizon. Facing away from the elevated celestial pole, an observer sees
the Sun, Moon, planets, and stars rise in the east and set in the west.
They reach their highest altitude as they cross the local meridian.
When the observer turns to face the elevated celestial pole, stars
nearest the pole neither rise nor set. They become circumpolar and
cross the meridian each day once above the pole at their highest
altitude and once below the pole at their lowest altitude. In the
Northern Hemisphere, circumpolar stars appear to rotate about the north
celestial pole counterclockwise. In the Southern Hemisphere the effect
is reversed and they appear to rotate clockwise.
Superimposed on the diurnal rotation is an annual rotation caused by
the Earth's orbiting the Sun. Since the stars are seen by the naked eye
after sunset, the constellations appear to move from east to west, and
to return to the same position after a year. Relative to the Sun, the
stars rise and set roughly four minutes earlier each day. In the course
of a month, the night sky appears to move two hours in right ascension
to the west. Also because of this orbital motion of the Earth, the
circumpolar stars in the Northern Hemisphere appear to rotate once a
year in a counterclockwise direction around the north celestial pole
and in a clockwise direction about the south celestial pole.
The Moon moves in an orbit inclined to the ecliptic by 5+ degrees; the
Moon makes one revolution about the sky from west to east in about a
month. During this period the phases on the Moon complete a cycle from
new to full and back to new. The orbit of the Moon is moving around the
ecliptic, so that other aspects of the Moon's position in the sky, such
as its maximum and minimum declination, change from one month the next.
The Sun, Moon and the Earth occasionally line up creating the phenomena
we call eclipses. Below is a graphic summary of eclipses for several
years.
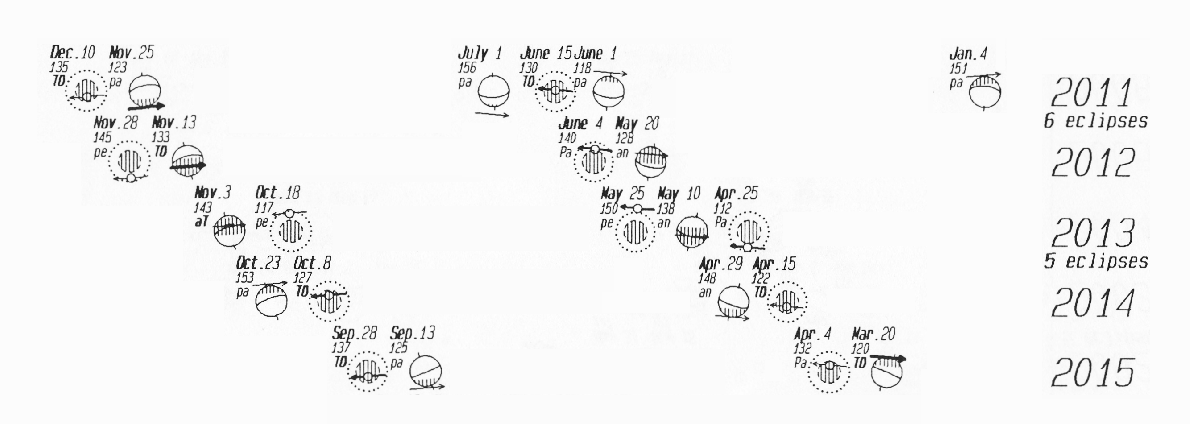 The above diagram, read from right to left, shows both solar and lunar
eclipse events for each of the years. Study the diagram carefully.
For solar eclipses, the shadow of the Moon sweeps across the surface of
the Earth. We are looking toward the Earth from the Sun (or Moon). The
Earth's equator is shown as well as one of its poles.
During a lunar eclipse, the Moon passes through the Earth's shadow. Our
perspective is looking toward the Moon from the night-time side of the
Earth. We see the Earth's shadow with respect to the smaller Moon. The
dotted line represents the outer edge of the penumbra, a region where
the sun is partially blocked by the Earth. The more shaded region in
the center is called the umbra--all sunlight is blocked by the Earth.
Newton's Laws
p = mv
This equation says that the momentum of a body is the product of its
mass and its velocity. If this were a calculus based course, I would be
obliged to tell you that this equation involves a time derivative,
where Newton defined velocity v = dr/dt .
Newton's first law, also called the "law of inertia", states that body
at rest remains at rest and a body in motion continues to move at a
constant velocity unless acted upon by an external force.
Conservation of momentum, embodied in Newton's first law, is a
fundamental law of physics which states that the momentum of a system
is constant if there are no external forces acting on the system.
F = dp/dt (Newton wrote)
F = ma (Euler's version) (5.1)
Either equation (after all they are equivalent) relates force, mass and
acceleration. Again, if this were a calculus based course, I would be
obliged to tell you that this equation involves a time derivative,
where the velocity a = dv/dt. In Euler's version on Newton's second
law, F is the applied force, m is the mass of the particle, and a is
the particle's acceleration.
F12 = -F21
Whenever a body exerts a force on another body, the latter exerts a
force of equal magnitude and opposite direction on the former. This is
known as the weak law of action and reaction.
Fgrav = G m1 m2 / r2 (5.2)
Gravity is the force exerted by all objects having mass on all other
objects having mass. Newton's Law of Gravitation says that the
gravitational force between to masses is proportional to their masses
and inversely proportional to the square of the distance between them.
Newton's Law of Gravitation incorporates the inverse-square law,
which states that some physical quantity or strength is inversely
proportional to the square of the distance from the source of that
physical quantity. Gravity, light, and sound all obey the
inverse-square law.
Homework Problems
You are expected to do all of your own homework. Statistical patterns
showing copying or collaboration will result in no credit for the
homework assignment for all participants involved. The Code of Academic
Conduct for Iowa Valley Community College District is found in the
Student Handbook. Please read it over.
Physical Science classes require the use of mathematics. If you don't
know algebra, you sould NOT be taking this class. If you need to review,
look at Introduction to Algebra
http://www.math.armstrong.edu/MathTutorial/
WolframAlpha is way faster than a scientific calculator.
http://www.wolframalpha.com
There is little excuse for turning homework in late. You have a whole
week between classes to read the chapters and do the homework. Homework
one week late - half credit. Two or more weeks late - no credit. Do the
homework during the week, not in class! You got homework questions,
email me 24/7. sam.wormley@gmail.com Even if you don't have a homework
Problem 1:
Explain clearly the differences between a sidereal day and a solar
day. Hint: You could give a definition for both. A diagram might be
helpful.
Problem 2:
Using the graphic summary of eclipses (above), what will be the
first total lunar eclipse to occur after your next birthday?
Important: for me to grade you on this and several other home work
problems, I need you to write your date of birth.
Date of Birth (MM/DD/YYYY): _____________________________
Problem 3:
Using a ruler, measure the eccentricities of all three ellipses
shown in Figure 4.13 on page 69. Hint: There are two ways you can
approach this problem. Remember that every ellipse has a semimajor
axis, a, and a semiminor axis, b, where the eccentricity e can be found
by the following formula:
e2 = (a2 - b2) / a2
The above diagram, read from right to left, shows both solar and lunar
eclipse events for each of the years. Study the diagram carefully.
For solar eclipses, the shadow of the Moon sweeps across the surface of
the Earth. We are looking toward the Earth from the Sun (or Moon). The
Earth's equator is shown as well as one of its poles.
During a lunar eclipse, the Moon passes through the Earth's shadow. Our
perspective is looking toward the Moon from the night-time side of the
Earth. We see the Earth's shadow with respect to the smaller Moon. The
dotted line represents the outer edge of the penumbra, a region where
the sun is partially blocked by the Earth. The more shaded region in
the center is called the umbra--all sunlight is blocked by the Earth.
Newton's Laws
p = mv
This equation says that the momentum of a body is the product of its
mass and its velocity. If this were a calculus based course, I would be
obliged to tell you that this equation involves a time derivative,
where Newton defined velocity v = dr/dt .
Newton's first law, also called the "law of inertia", states that body
at rest remains at rest and a body in motion continues to move at a
constant velocity unless acted upon by an external force.
Conservation of momentum, embodied in Newton's first law, is a
fundamental law of physics which states that the momentum of a system
is constant if there are no external forces acting on the system.
F = dp/dt (Newton wrote)
F = ma (Euler's version) (5.1)
Either equation (after all they are equivalent) relates force, mass and
acceleration. Again, if this were a calculus based course, I would be
obliged to tell you that this equation involves a time derivative,
where the velocity a = dv/dt. In Euler's version on Newton's second
law, F is the applied force, m is the mass of the particle, and a is
the particle's acceleration.
F12 = -F21
Whenever a body exerts a force on another body, the latter exerts a
force of equal magnitude and opposite direction on the former. This is
known as the weak law of action and reaction.
Fgrav = G m1 m2 / r2 (5.2)
Gravity is the force exerted by all objects having mass on all other
objects having mass. Newton's Law of Gravitation says that the
gravitational force between to masses is proportional to their masses
and inversely proportional to the square of the distance between them.
Newton's Law of Gravitation incorporates the inverse-square law,
which states that some physical quantity or strength is inversely
proportional to the square of the distance from the source of that
physical quantity. Gravity, light, and sound all obey the
inverse-square law.
Homework Problems
You are expected to do all of your own homework. Statistical patterns
showing copying or collaboration will result in no credit for the
homework assignment for all participants involved. The Code of Academic
Conduct for Iowa Valley Community College District is found in the
Student Handbook. Please read it over.
Physical Science classes require the use of mathematics. If you don't
know algebra, you sould NOT be taking this class. If you need to review,
look at Introduction to Algebra
http://www.math.armstrong.edu/MathTutorial/
WolframAlpha is way faster than a scientific calculator.
http://www.wolframalpha.com
There is little excuse for turning homework in late. You have a whole
week between classes to read the chapters and do the homework. Homework
one week late - half credit. Two or more weeks late - no credit. Do the
homework during the week, not in class! You got homework questions,
email me 24/7. sam.wormley@gmail.com Even if you don't have a homework
Problem 1:
Explain clearly the differences between a sidereal day and a solar
day. Hint: You could give a definition for both. A diagram might be
helpful.
Problem 2:
Using the graphic summary of eclipses (above), what will be the
first total lunar eclipse to occur after your next birthday?
Important: for me to grade you on this and several other home work
problems, I need you to write your date of birth.
Date of Birth (MM/DD/YYYY): _____________________________
Problem 3:
Using a ruler, measure the eccentricities of all three ellipses
shown in Figure 4.13 on page 69. Hint: There are two ways you can
approach this problem. Remember that every ellipse has a semimajor
axis, a, and a semiminor axis, b, where the eccentricity e can be found
by the following formula:
e2 = (a2 - b2) / a2
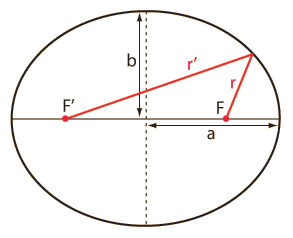 See: http://mathworld.wolfram.com/Ellipse.html
Perhaps a simpler method is measuring the distance between the foci and
dividing that by the largest diameter (2a) of the ellipse. Either
method should give the same result. It doesn't matter what units of
measure you use: inches, mm, pencil widths, or eyelash lengths.
Problem 4:
Hold out your thumb again. Beyond your thumb look at an object further
away, such as a chair or tree. While focusing on the more distant
object, notice there are two images of your thumb. Now focus on your
thumb and notice there are two images of the chair or tree in the
distance. That's Parallax.
See: http://mathworld.wolfram.com/Ellipse.html
Perhaps a simpler method is measuring the distance between the foci and
dividing that by the largest diameter (2a) of the ellipse. Either
method should give the same result. It doesn't matter what units of
measure you use: inches, mm, pencil widths, or eyelash lengths.
Problem 4:
Hold out your thumb again. Beyond your thumb look at an object further
away, such as a chair or tree. While focusing on the more distant
object, notice there are two images of your thumb. Now focus on your
thumb and notice there are two images of the chair or tree in the
distance. That's Parallax.
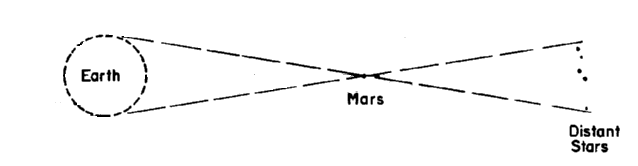 Tycho Brahe was trying to measure the parallax of Mars. In order to do
this he would make observations of Mars when it was near opposition
during the same night as the Earth turns, giving him two perspectives.
Tycho (pronounced TEE-KOH) was able to routinely measure the positions
of stars and planets in the sky with an accuracy of two minutes of
arc.
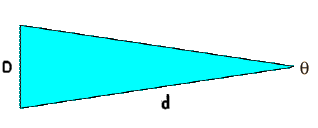
Could Tycho, given his two minutes of arc accuracy, have found the
parallax of Mars? Hint: to answer the question solve for the small
angle using the diameter of the Earth, D, and the distance between
Earth and Mars at opposition d. Unless you know trig, use the small
angle formula (3.1) from your textbook shown on page 45.
Tycho Brahe was trying to measure the parallax of Mars. In order to do
this he would make observations of Mars when it was near opposition
during the same night as the Earth turns, giving him two perspectives.
Tycho (pronounced TEE-KOH) was able to routinely measure the positions
of stars and planets in the sky with an accuracy of two minutes of
arc.
Could Tycho, given his two minutes of arc accuracy, have found the
parallax of Mars? Hint: to answer the question solve for the small
angle using the diameter of the Earth, D, and the distance between
Earth and Mars at opposition d. Unless you know trig, use the small
angle formula (3.1) from your textbook shown on page 45.
 http://www.google.com/search?q=tan+%282*+6378.137+km+%2F+0.5+AU%29+in+arc+minutes
http://www.google.com/search?q=2*206265+arc+seconds+*6378.137+km%2F.5+AU+in+arc+minutes
Problem 5:
Looking at Newton's Law of Gravitation
Fgrav = G m1 m2 / r2
where F is the force of gravity between two masses m1 and m2, G is
Newton's Gravitational Constant, and r is the separation of the two
masses, What happens to the F, the force of gravity, if r is reduced
by half?
Problem 6:
Using your planisphere (starwheel), place the star, Vega, on your
local meridian, so that Vega is transiting. What time does Vega transit
on your birthday?
Problem 7:
The one equation that is at the heart of orbital mechanics is Newton's
second law of motion. This law tells us that applying a force, F to an
object with mass, m causes it to accelerate, a.
F = ma
Another key equation that Newton handed down to us is his law of
universal gravitation. In this relationship, Newton describes the
mutual attraction between two objects with mass. Simply put, the law of
universal gravitation says that two objects having mass m1 and m2 and
separated by a distance r are attracted to each other with equal and
opposite forces directed along the line joining the objects. The
magnitude of that force, F is given by:
Fgrav = G m1 m2 / r2
Based on Newton's equations, we can derive an expression for orbital
speed of a circular orbit.
vc = SQRT (GM/r) (5.5), pg 91
Determine how fast the astronauts are "flying" when in the
International Space Station (ISS) or in the Space Shuttle. Hint use
an orbital radius of 324 km (elevation) + 6378.137 km (Earth's radius)
or about 6702 km.
Problem 8:
Using Isaac Newton's formulation for Kepler's third law (see
equation 5.4 on page 90 of your textbook), Determine the orbital period
for the astronauts while in orbit. Hint: ignore the little m in the
equation as it is insignificant. Use the mass of the Earth for the big
M.
Problem 9:
Assume that the Local Sidereal Time (LST) is 5h 10m. Using your
planisphere, determine how many minutes later, the star, Markab, will
set. Hint: Markab is one of the corner stars in the great square of
Pegasus. Also the Local Sidereal Time (LST) is simply the Right
Ascension of the sky (stars) currently on your local meridian.
Problem 10:
Suppose that the distance between two stars is doubled while the
mass of each star is doubled as well. What would happen to the orbital
period of the two stars? Hint: What happens to the left side of
Newton's version of Kepler's third law (5.4) on page 90 if you put some
factors of 2 into the right hand side?
http://www.google.com/search?q=tan+%282*+6378.137+km+%2F+0.5+AU%29+in+arc+minutes
http://www.google.com/search?q=2*206265+arc+seconds+*6378.137+km%2F.5+AU+in+arc+minutes
Problem 5:
Looking at Newton's Law of Gravitation
Fgrav = G m1 m2 / r2
where F is the force of gravity between two masses m1 and m2, G is
Newton's Gravitational Constant, and r is the separation of the two
masses, What happens to the F, the force of gravity, if r is reduced
by half?
Problem 6:
Using your planisphere (starwheel), place the star, Vega, on your
local meridian, so that Vega is transiting. What time does Vega transit
on your birthday?
Problem 7:
The one equation that is at the heart of orbital mechanics is Newton's
second law of motion. This law tells us that applying a force, F to an
object with mass, m causes it to accelerate, a.
F = ma
Another key equation that Newton handed down to us is his law of
universal gravitation. In this relationship, Newton describes the
mutual attraction between two objects with mass. Simply put, the law of
universal gravitation says that two objects having mass m1 and m2 and
separated by a distance r are attracted to each other with equal and
opposite forces directed along the line joining the objects. The
magnitude of that force, F is given by:
Fgrav = G m1 m2 / r2
Based on Newton's equations, we can derive an expression for orbital
speed of a circular orbit.
vc = SQRT (GM/r) (5.5), pg 91
Determine how fast the astronauts are "flying" when in the
International Space Station (ISS) or in the Space Shuttle. Hint use
an orbital radius of 324 km (elevation) + 6378.137 km (Earth's radius)
or about 6702 km.
Problem 8:
Using Isaac Newton's formulation for Kepler's third law (see
equation 5.4 on page 90 of your textbook), Determine the orbital period
for the astronauts while in orbit. Hint: ignore the little m in the
equation as it is insignificant. Use the mass of the Earth for the big
M.
Problem 9:
Assume that the Local Sidereal Time (LST) is 5h 10m. Using your
planisphere, determine how many minutes later, the star, Markab, will
set. Hint: Markab is one of the corner stars in the great square of
Pegasus. Also the Local Sidereal Time (LST) is simply the Right
Ascension of the sky (stars) currently on your local meridian.
Problem 10:
Suppose that the distance between two stars is doubled while the
mass of each star is doubled as well. What would happen to the orbital
period of the two stars? Hint: What happens to the left side of
Newton's version of Kepler's third law (5.4) on page 90 if you put some
factors of 2 into the right hand side?
 Apparent Motions of the Sky (cont.)
The Earth rotates about its polar axis once a day and produces an
apparent motion on the night sky about the celestial poles. In the
Northern Hemisphere the north celestial pole is elevated above the
horizon. Facing away from the elevated celestial pole, an observer sees
the Sun, Moon, planets, and stars rise in the east and set in the west.
They reach their highest altitude as they cross the local meridian.
When the observer turns to face the elevated celestial pole, stars
nearest the pole neither rise nor set. They become circumpolar and
cross the meridian each day once above the pole at their highest
altitude and once below the pole at their lowest altitude. In the
Northern Hemisphere, circumpolar stars appear to rotate about the north
celestial pole counterclockwise. In the Southern Hemisphere the effect
is reversed and they appear to rotate clockwise.
Superimposed on the diurnal rotation is an annual rotation caused by
the Earth's orbiting the Sun. Since the stars are seen by the naked eye
after sunset, the constellations appear to move from east to west, and
to return to the same position after a year. Relative to the Sun, the
stars rise and set roughly four minutes earlier each day. In the course
of a month, the night sky appears to move two hours in right ascension
to the west. Also because of this orbital motion of the Earth, the
circumpolar stars in the Northern Hemisphere appear to rotate once a
year in a counterclockwise direction around the north celestial pole
and in a clockwise direction about the south celestial pole.
The Moon moves in an orbit inclined to the ecliptic by 5+ degrees; the
Moon makes one revolution about the sky from west to east in about a
month. During this period the phases on the Moon complete a cycle from
new to full and back to new. The orbit of the Moon is moving around the
ecliptic, so that other aspects of the Moon's position in the sky, such
as its maximum and minimum declination, change from one month the next.
The Sun, Moon and the Earth occasionally line up creating the phenomena
we call eclipses. Below is a graphic summary of eclipses for several
years.
Apparent Motions of the Sky (cont.)
The Earth rotates about its polar axis once a day and produces an
apparent motion on the night sky about the celestial poles. In the
Northern Hemisphere the north celestial pole is elevated above the
horizon. Facing away from the elevated celestial pole, an observer sees
the Sun, Moon, planets, and stars rise in the east and set in the west.
They reach their highest altitude as they cross the local meridian.
When the observer turns to face the elevated celestial pole, stars
nearest the pole neither rise nor set. They become circumpolar and
cross the meridian each day once above the pole at their highest
altitude and once below the pole at their lowest altitude. In the
Northern Hemisphere, circumpolar stars appear to rotate about the north
celestial pole counterclockwise. In the Southern Hemisphere the effect
is reversed and they appear to rotate clockwise.
Superimposed on the diurnal rotation is an annual rotation caused by
the Earth's orbiting the Sun. Since the stars are seen by the naked eye
after sunset, the constellations appear to move from east to west, and
to return to the same position after a year. Relative to the Sun, the
stars rise and set roughly four minutes earlier each day. In the course
of a month, the night sky appears to move two hours in right ascension
to the west. Also because of this orbital motion of the Earth, the
circumpolar stars in the Northern Hemisphere appear to rotate once a
year in a counterclockwise direction around the north celestial pole
and in a clockwise direction about the south celestial pole.
The Moon moves in an orbit inclined to the ecliptic by 5+ degrees; the
Moon makes one revolution about the sky from west to east in about a
month. During this period the phases on the Moon complete a cycle from
new to full and back to new. The orbit of the Moon is moving around the
ecliptic, so that other aspects of the Moon's position in the sky, such
as its maximum and minimum declination, change from one month the next.
The Sun, Moon and the Earth occasionally line up creating the phenomena
we call eclipses. Below is a graphic summary of eclipses for several
years.
 The above diagram, read from right to left, shows both solar and lunar
eclipse events for each of the years. Study the diagram carefully.
For solar eclipses, the shadow of the Moon sweeps across the surface of
the Earth. We are looking toward the Earth from the Sun (or Moon). The
Earth's equator is shown as well as one of its poles.
During a lunar eclipse, the Moon passes through the Earth's shadow. Our
perspective is looking toward the Moon from the night-time side of the
Earth. We see the Earth's shadow with respect to the smaller Moon. The
dotted line represents the outer edge of the penumbra, a region where
the sun is partially blocked by the Earth. The more shaded region in
the center is called the umbra--all sunlight is blocked by the Earth.
Newton's Laws
p = mv
This equation says that the momentum of a body is the product of its
mass and its velocity. If this were a calculus based course, I would be
obliged to tell you that this equation involves a time derivative,
where Newton defined velocity v = dr/dt .
Newton's first law, also called the "law of inertia", states that body
at rest remains at rest and a body in motion continues to move at a
constant velocity unless acted upon by an external force.
Conservation of momentum, embodied in Newton's first law, is a
fundamental law of physics which states that the momentum of a system
is constant if there are no external forces acting on the system.
F = dp/dt (Newton wrote)
F = ma (Euler's version) (5.1)
Either equation (after all they are equivalent) relates force, mass and
acceleration. Again, if this were a calculus based course, I would be
obliged to tell you that this equation involves a time derivative,
where the velocity a = dv/dt. In Euler's version on Newton's second
law, F is the applied force, m is the mass of the particle, and a is
the particle's acceleration.
F12 = -F21
Whenever a body exerts a force on another body, the latter exerts a
force of equal magnitude and opposite direction on the former. This is
known as the weak law of action and reaction.
Fgrav = G m1 m2 / r2 (5.2)
Gravity is the force exerted by all objects having mass on all other
objects having mass. Newton's Law of Gravitation says that the
gravitational force between to masses is proportional to their masses
and inversely proportional to the square of the distance between them.
Newton's Law of Gravitation incorporates the inverse-square law,
which states that some physical quantity or strength is inversely
proportional to the square of the distance from the source of that
physical quantity. Gravity, light, and sound all obey the
inverse-square law.
Homework Problems
You are expected to do all of your own homework. Statistical patterns
showing copying or collaboration will result in no credit for the
homework assignment for all participants involved. The Code of Academic
Conduct for Iowa Valley Community College District is found in the
Student Handbook. Please read it over.
Physical Science classes require the use of mathematics. If you don't
know algebra, you sould NOT be taking this class. If you need to review,
look at Introduction to Algebra
http://www.math.armstrong.edu/MathTutorial/
WolframAlpha is way faster than a scientific calculator.
http://www.wolframalpha.com
There is little excuse for turning homework in late. You have a whole
week between classes to read the chapters and do the homework. Homework
one week late - half credit. Two or more weeks late - no credit. Do the
homework during the week, not in class! You got homework questions,
email me 24/7. sam.wormley@gmail.com Even if you don't have a homework
Problem 1:
Explain clearly the differences between a sidereal day and a solar
day. Hint: You could give a definition for both. A diagram might be
helpful.
Problem 2:
Using the graphic summary of eclipses (above), what will be the
first total lunar eclipse to occur after your next birthday?
Important: for me to grade you on this and several other home work
problems, I need you to write your date of birth.
Date of Birth (MM/DD/YYYY): _____________________________
Problem 3:
Using a ruler, measure the eccentricities of all three ellipses
shown in Figure 4.13 on page 69. Hint: There are two ways you can
approach this problem. Remember that every ellipse has a semimajor
axis, a, and a semiminor axis, b, where the eccentricity e can be found
by the following formula:
e2 = (a2 - b2) / a2
The above diagram, read from right to left, shows both solar and lunar
eclipse events for each of the years. Study the diagram carefully.
For solar eclipses, the shadow of the Moon sweeps across the surface of
the Earth. We are looking toward the Earth from the Sun (or Moon). The
Earth's equator is shown as well as one of its poles.
During a lunar eclipse, the Moon passes through the Earth's shadow. Our
perspective is looking toward the Moon from the night-time side of the
Earth. We see the Earth's shadow with respect to the smaller Moon. The
dotted line represents the outer edge of the penumbra, a region where
the sun is partially blocked by the Earth. The more shaded region in
the center is called the umbra--all sunlight is blocked by the Earth.
Newton's Laws
p = mv
This equation says that the momentum of a body is the product of its
mass and its velocity. If this were a calculus based course, I would be
obliged to tell you that this equation involves a time derivative,
where Newton defined velocity v = dr/dt .
Newton's first law, also called the "law of inertia", states that body
at rest remains at rest and a body in motion continues to move at a
constant velocity unless acted upon by an external force.
Conservation of momentum, embodied in Newton's first law, is a
fundamental law of physics which states that the momentum of a system
is constant if there are no external forces acting on the system.
F = dp/dt (Newton wrote)
F = ma (Euler's version) (5.1)
Either equation (after all they are equivalent) relates force, mass and
acceleration. Again, if this were a calculus based course, I would be
obliged to tell you that this equation involves a time derivative,
where the velocity a = dv/dt. In Euler's version on Newton's second
law, F is the applied force, m is the mass of the particle, and a is
the particle's acceleration.
F12 = -F21
Whenever a body exerts a force on another body, the latter exerts a
force of equal magnitude and opposite direction on the former. This is
known as the weak law of action and reaction.
Fgrav = G m1 m2 / r2 (5.2)
Gravity is the force exerted by all objects having mass on all other
objects having mass. Newton's Law of Gravitation says that the
gravitational force between to masses is proportional to their masses
and inversely proportional to the square of the distance between them.
Newton's Law of Gravitation incorporates the inverse-square law,
which states that some physical quantity or strength is inversely
proportional to the square of the distance from the source of that
physical quantity. Gravity, light, and sound all obey the
inverse-square law.
Homework Problems
You are expected to do all of your own homework. Statistical patterns
showing copying or collaboration will result in no credit for the
homework assignment for all participants involved. The Code of Academic
Conduct for Iowa Valley Community College District is found in the
Student Handbook. Please read it over.
Physical Science classes require the use of mathematics. If you don't
know algebra, you sould NOT be taking this class. If you need to review,
look at Introduction to Algebra
http://www.math.armstrong.edu/MathTutorial/
WolframAlpha is way faster than a scientific calculator.
http://www.wolframalpha.com
There is little excuse for turning homework in late. You have a whole
week between classes to read the chapters and do the homework. Homework
one week late - half credit. Two or more weeks late - no credit. Do the
homework during the week, not in class! You got homework questions,
email me 24/7. sam.wormley@gmail.com Even if you don't have a homework
Problem 1:
Explain clearly the differences between a sidereal day and a solar
day. Hint: You could give a definition for both. A diagram might be
helpful.
Problem 2:
Using the graphic summary of eclipses (above), what will be the
first total lunar eclipse to occur after your next birthday?
Important: for me to grade you on this and several other home work
problems, I need you to write your date of birth.
Date of Birth (MM/DD/YYYY): _____________________________
Problem 3:
Using a ruler, measure the eccentricities of all three ellipses
shown in Figure 4.13 on page 69. Hint: There are two ways you can
approach this problem. Remember that every ellipse has a semimajor
axis, a, and a semiminor axis, b, where the eccentricity e can be found
by the following formula:
e2 = (a2 - b2) / a2
 See: http://mathworld.wolfram.com/Ellipse.html
Perhaps a simpler method is measuring the distance between the foci and
dividing that by the largest diameter (2a) of the ellipse. Either
method should give the same result. It doesn't matter what units of
measure you use: inches, mm, pencil widths, or eyelash lengths.
Problem 4:
Hold out your thumb again. Beyond your thumb look at an object further
away, such as a chair or tree. While focusing on the more distant
object, notice there are two images of your thumb. Now focus on your
thumb and notice there are two images of the chair or tree in the
distance. That's Parallax.
See: http://mathworld.wolfram.com/Ellipse.html
Perhaps a simpler method is measuring the distance between the foci and
dividing that by the largest diameter (2a) of the ellipse. Either
method should give the same result. It doesn't matter what units of
measure you use: inches, mm, pencil widths, or eyelash lengths.
Problem 4:
Hold out your thumb again. Beyond your thumb look at an object further
away, such as a chair or tree. While focusing on the more distant
object, notice there are two images of your thumb. Now focus on your
thumb and notice there are two images of the chair or tree in the
distance. That's Parallax.
 Tycho Brahe was trying to measure the parallax of Mars. In order to do
this he would make observations of Mars when it was near opposition
during the same night as the Earth turns, giving him two perspectives.
Tycho (pronounced TEE-KOH) was able to routinely measure the positions
of stars and planets in the sky with an accuracy of two minutes of
arc.
Could Tycho, given his two minutes of arc accuracy, have found the
parallax of Mars? Hint: to answer the question solve for the small
angle using the diameter of the Earth, D, and the distance between
Earth and Mars at opposition d. Unless you know trig, use the small
angle formula (3.1) from your textbook shown on page 45.
Tycho Brahe was trying to measure the parallax of Mars. In order to do
this he would make observations of Mars when it was near opposition
during the same night as the Earth turns, giving him two perspectives.
Tycho (pronounced TEE-KOH) was able to routinely measure the positions
of stars and planets in the sky with an accuracy of two minutes of
arc.
Could Tycho, given his two minutes of arc accuracy, have found the
parallax of Mars? Hint: to answer the question solve for the small
angle using the diameter of the Earth, D, and the distance between
Earth and Mars at opposition d. Unless you know trig, use the small
angle formula (3.1) from your textbook shown on page 45.
 http://www.google.com/search?q=tan+%282*+6378.137+km+%2F+0.5+AU%29+in+arc+minutes
http://www.google.com/search?q=2*206265+arc+seconds+*6378.137+km%2F.5+AU+in+arc+minutes
Problem 5:
Looking at Newton's Law of Gravitation
Fgrav = G m1 m2 / r2
where F is the force of gravity between two masses m1 and m2, G is
Newton's Gravitational Constant, and r is the separation of the two
masses, What happens to the F, the force of gravity, if r is reduced
by half?
Problem 6:
Using your planisphere (starwheel), place the star, Vega, on your
local meridian, so that Vega is transiting. What time does Vega transit
on your birthday?
Problem 7:
The one equation that is at the heart of orbital mechanics is Newton's
second law of motion. This law tells us that applying a force, F to an
object with mass, m causes it to accelerate, a.
F = ma
Another key equation that Newton handed down to us is his law of
universal gravitation. In this relationship, Newton describes the
mutual attraction between two objects with mass. Simply put, the law of
universal gravitation says that two objects having mass m1 and m2 and
separated by a distance r are attracted to each other with equal and
opposite forces directed along the line joining the objects. The
magnitude of that force, F is given by:
Fgrav = G m1 m2 / r2
Based on Newton's equations, we can derive an expression for orbital
speed of a circular orbit.
vc = SQRT (GM/r) (5.5), pg 91
Determine how fast the astronauts are "flying" when in the
International Space Station (ISS) or in the Space Shuttle. Hint use
an orbital radius of 324 km (elevation) + 6378.137 km (Earth's radius)
or about 6702 km.
Problem 8:
Using Isaac Newton's formulation for Kepler's third law (see
equation 5.4 on page 90 of your textbook), Determine the orbital period
for the astronauts while in orbit. Hint: ignore the little m in the
equation as it is insignificant. Use the mass of the Earth for the big
M.
Problem 9:
Assume that the Local Sidereal Time (LST) is 5h 10m. Using your
planisphere, determine how many minutes later, the star, Markab, will
set. Hint: Markab is one of the corner stars in the great square of
Pegasus. Also the Local Sidereal Time (LST) is simply the Right
Ascension of the sky (stars) currently on your local meridian.
Problem 10:
Suppose that the distance between two stars is doubled while the
mass of each star is doubled as well. What would happen to the orbital
period of the two stars? Hint: What happens to the left side of
Newton's version of Kepler's third law (5.4) on page 90 if you put some
factors of 2 into the right hand side?
http://www.google.com/search?q=tan+%282*+6378.137+km+%2F+0.5+AU%29+in+arc+minutes
http://www.google.com/search?q=2*206265+arc+seconds+*6378.137+km%2F.5+AU+in+arc+minutes
Problem 5:
Looking at Newton's Law of Gravitation
Fgrav = G m1 m2 / r2
where F is the force of gravity between two masses m1 and m2, G is
Newton's Gravitational Constant, and r is the separation of the two
masses, What happens to the F, the force of gravity, if r is reduced
by half?
Problem 6:
Using your planisphere (starwheel), place the star, Vega, on your
local meridian, so that Vega is transiting. What time does Vega transit
on your birthday?
Problem 7:
The one equation that is at the heart of orbital mechanics is Newton's
second law of motion. This law tells us that applying a force, F to an
object with mass, m causes it to accelerate, a.
F = ma
Another key equation that Newton handed down to us is his law of
universal gravitation. In this relationship, Newton describes the
mutual attraction between two objects with mass. Simply put, the law of
universal gravitation says that two objects having mass m1 and m2 and
separated by a distance r are attracted to each other with equal and
opposite forces directed along the line joining the objects. The
magnitude of that force, F is given by:
Fgrav = G m1 m2 / r2
Based on Newton's equations, we can derive an expression for orbital
speed of a circular orbit.
vc = SQRT (GM/r) (5.5), pg 91
Determine how fast the astronauts are "flying" when in the
International Space Station (ISS) or in the Space Shuttle. Hint use
an orbital radius of 324 km (elevation) + 6378.137 km (Earth's radius)
or about 6702 km.
Problem 8:
Using Isaac Newton's formulation for Kepler's third law (see
equation 5.4 on page 90 of your textbook), Determine the orbital period
for the astronauts while in orbit. Hint: ignore the little m in the
equation as it is insignificant. Use the mass of the Earth for the big
M.
Problem 9:
Assume that the Local Sidereal Time (LST) is 5h 10m. Using your
planisphere, determine how many minutes later, the star, Markab, will
set. Hint: Markab is one of the corner stars in the great square of
Pegasus. Also the Local Sidereal Time (LST) is simply the Right
Ascension of the sky (stars) currently on your local meridian.
Problem 10:
Suppose that the distance between two stars is doubled while the
mass of each star is doubled as well. What would happen to the orbital
period of the two stars? Hint: What happens to the left side of
Newton's version of Kepler's third law (5.4) on page 90 if you put some
factors of 2 into the right hand side?