MCC PHS 142 M01 Astronomy Homework Ch.24-25
Adj Prof Astronomy: Sam Wormley <sam.wormley@gmail.com>
Web: edu-observatory.org
Background Material
Textbook - Read Chapters 24-25
Textbook - http://highered.mcgraw-hill.com/sites/0073512184/student_view0/chapter24/
Textbook - http://highered.mcgraw-hill.com/sites/0073512184/student_view0/chapter25/
(take the Multiple Choice Quiz for for each chapter)
Web - http://edu-observatory.org/eo/cosmology.html
Web - http://edu-observatory.org/eo/galaxies.html
Web - http://edu-observatory.org/eo/radio_astronomy.html
Web - http://www.astro.ucla.edu/~wright/cosmolog.htm
Web - http://antwrp.gsfc.nasa.gov/apod/archivepix.html
"We shall probably never know whether the first men and women to walk
on this planet a few million years ago asked themselves questions about
the sun, the moon, the stars. But from the time that the last ice age
receded, 10,000 years ago, and human beings began to practice
agriculture, we can be sure that they were interested in the seasons
and the calendar. There is abundant evidence of astronomical purpose in
the most ancient of the stone-age monuments of 3000 B.C.[E.] or so. We
know that by 2000 B.C.[E.] the Babylonians were regularly observing
Venus, and by the time of the height of the Babylonian civilization,
around 600 B.C.[E.], we find sophisticated astronomical knowledge among
both the Babylonians and the Chinese.
"The intellectual horizon of the human race at any time has always been
inextricably bound up with the perceived scale of the universe. Ancient
myths and those of surviving primitive peoples in or own times suggest
a conception of the heavens as not very far off at all. For example, in
the most antique of the Chinese cosmologies, the Kai Thien or
hemispherical dome theory, the heavens are seen as a rotating
hemispherical cover, the earth as a bowl turned upside down, and the
distance between the two as considerably less than the radius of the
earth. Stories in which the sun or moon is carried in a chariot or boat
suggest a distance scale measured on an even smaller, human scale. And
there can be little doubt that a people's perceived scale of the
universe must play a fundamental role in its culture and
consciousness.
"It is tempting to consider the growth of knowledge as a linear
progress and to consider ourselves as therefore intellectually superior
to the ancients. This fallacy is fueled by a picture of science,
surprisingly widely held among scientists today, as data collection and
analysis. The accumulation of data does indeed proceed monotonically,
but science consists of ideas that give meaning to these data, not the
data themselves. When we look at the history of ideas about the scale
of the universe, we find that the modern idea of an infinite universe
through which countless stars and planets wander is not modern at all,
but was held firmly by the Greek atomists and by the Chinese
cosmologists of the Hsuan Yeh school. And even Aristotle, whom we have
been taught to regard as the obstacle to scientific progress in the
Middle Ages, summarized the views of his contemporaries in a way that
could easily be adapted to modern cosmological prediction: "All
thinkers agree that the world has a beginning, but some maintain that
having begun, it is everlasting, others that it is perishable like any
other formation of matter, and others again that it alternates, being
at one time as it is now, and at another time changing and perishing,
and that this process continues unremittingly."
-Michael Rowan-Robinson
The Cosmological Distance Ladder
One of the most important, although difficult, tasks that astronomers
have undertaken in the twentieth century has been the determination of
the distances to the galaxies. This work is of special importance
because galaxies and clusters of galaxies mark the basic structure of
the universe. Thus our ability to answer fundamental questions about
the origin and fate of the universe depends on how well we know the
distances of galaxies.
The size of the solar system--a first requirement for the establishment
of a cosmic distance scale is the correct measurement of distances
within the solar system. The basic step in this procedure is the
measurement of the distance to Venus. The most precise way of obtaining
this distance is through the use of radar techniques.
A radar pulse is sent out in the direction of Venus, and the time
between its transmission and reception is measured. Since time
measurements can be made with great accuracy, the distance to Venus and
the dimensions of its orbit can be established within a kilometer.
Once the distance to Venus is known at closest approach a, and most
distant separation b, and these measurements are repeated over a number
of years, the diameter and eccentricity of both the earth's and Venus s
orbit can be computed. The mean distance from the earth to the sun is
then directly available as the mean value of (a + b)/2. This distance
is called the astronomical unit. A check on the Earth-Venus distance is
obtained from trajectories of space vehicles sent to Venus.
When observations are made from opposite extremes in the earth's orbit
about the sun, a nearby star will appear displaced relative to more
distant stars in the same part of the sky. The parallax, p, is defined
as half the apparent angular displacement measured in this way. Look
closely at this diagram:
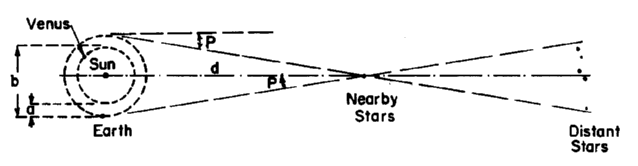The diagram may seem a little confusing, after all, I've been telling
you for weeks that one astronomical unit (1 AU) is the mean distance
between the Earth and Sun. And it is, but astronomers can determine 1
au more precisely as the mean value of (a + b)/2. I'm telling you this
just so you know. It's harder to make a direct and accurate measurement
from the Earth to the Sun. For one reason, the Sun doesn't have a
definite edge! What you care about is the relationship d, the distance
to a neighbor star, p, the parallax angle, and the radius of the
Earth's orbit, 1 AU. Here's the equation:
d = 1 astronomical unit / tan(p)
Look in Appendix 3 (Conversion Factors) in your textbook. Among those
factors, it says that one parsec (which is about 3.26 light years) is
equal to 206,265 AU. So you can see how much further stars are apart
compared to the planets around our Sun! The nearest star, Proxima
Centauri, is 4.24 light years away.
Once we know the distance to the nearest stars, by parallax methods, we
need other "yard sticks" to build our cosmological distance ladder.
Among the objects uses to determine cosmic distances, each kind of
object or technique can be used for a range of distances from the
nearest object of that type to the greatest distance at which that kind
of object can be seen. For instance, Cepheid variable stars, that are
discussed in chapters 19 and 24 of your textbook, can be used as
indicators for distances between a few hundred parsecs and a few tens
of megaparsecs.
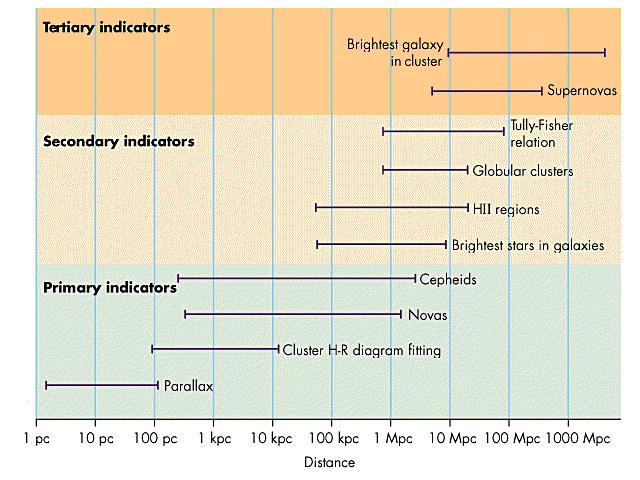Your textbook has a better diagram than this one on page 566 showing
which indicators are primary, secondary (based on primary) and tertiary
(based on secondary). If there are errors in the primary indicators,
then the secondary and tertiary indicators just exaggerate the error.
The cosmological distance ladder is painstakingly built up, from the
solar system up to the largest cosmological scale. The figure on page
545 gives an approximate summary of the cosmological distance ladder in
graphic form. Many of these methods can be pushed go greater distances
with improved technology and existing ground-based techniques. The
parallax an proper-motion satellite Hipparcos, launched in the late
1980's extended the parallax method to about 1000 light years. This new
precision, in turn, leads to a more fundamental calibration of Cepheid,
RR Lyrae, and nova methods. You saw in the "Mysteries of Deep Space"
work by Saul Perlmutter and Alexei V. Filippenko, who are trying to
measure the distance and recession velocity of Type Ia Supernovas more
than half way across the observable universe. [Did you know that if you
put the first four letters of the last names of Perlmutter, Filippenko
and Wormley in the American Astronomical Society's on-line directory at
http://directory.aas.org/ you get Saul, Alexei, and me!]
GRAVITATION AND INERTIA by Ignazio Ciufolini and John Archibald Wheeler
Princeton University Press, Princeton, NJ 1995
QC173.59.G44C58 1995
530.1 1--dc20 94-29874 CIP
ISBN 0-691-03323-4
In the first chapter Ciufolini and Wheeler introduce concepts and ideas
of Einstein's General Theory of Relativity which are developed in the
book. This is not an easy book to read for leisure due to the
mathematics that is typical in graduate level texts. However, the
elegance of conceptual explanation in the first chapter and throughout
the text makes this a book well worth reading. Part of the introductory
material is reproduced here, because it represents a very simple (yet
correct) overview of what General Relativity is and its relationship to
inertia. Think of a basketball sitting at the front end of a little
read wagon. When you start to pull the wagon forward, the ball tends to
stay put (looks like it's rolling to the back of the wagon). That is
inertia--the tendency of objects to resist a change of motion
(acceleration).
"Gravity is not a foreign and physical force transmitted through space
and time. It is a manifestation of the curvature of spacetime."
That, in a nutshell, is Einstein's theory.
What this theory is and what it means, we grasp more fully by looking
at its intellectual antecedents. First, there was the idea of Riemann
that space, telling mass how to move, must itself--by the principle of
action and reaction--be affected by mass. It cannot be an ideal
Euclidean perfection, standing in high mightiness above the battles of
matter and energy. Space geometry must be a participant in the world of
physics. Second, there was the contention of Ernst Mach that the
"acceleration relative to absolute space" of Newton is only properly
understood when it is viewed as acceleration relative to the sole
significant mass there really is, the distant stars. According to this
"Mach principle," inertia here arises from mass there. Third was that
great insight of Einstein that we summarize in the phrase "free fall is
free float": the equivalence principle, one of the best-tested
principles in physics, from the inclined tables of Galilei and the
pendulum experiments of Galilei, Huygens, and Newton to the highly
accurate torsion balance measurements of the twentieth century, and the
Lunar Laser Ranging experiment. With those three clues vibrating in his
head, the magic of the mind opened to Einstein what remains one of
mankind's most precious insights: gravity in manifestation of spacetime
curvature.
Euclid's (active around 300 B.C.) fifth postulate states that, given
any straight line and any point not on it, we can draw through that
point one and only one straight line parallel to the given line, that
is, a line that will never meet the given one (this alternative
formulation of the fifth postulate is essentially due to Proclos). This
is the parallel postulate. In the early 1800s the discussion grew
lively about whether the properties of parallel lines as presupposed in
Euclidean geometry could be derived from the other postulate and
axioms, or whether the parallel postulate had to be assumed
independently. More than two thousand years after Euclid, Karl
Friedrich Gauss, Jnos Bolyai, and Nikolai Ivanovich Lobacevskij
discovered pencil-and paper geometric systems that satisfy all the
axioms and postulates of Euclidean geometry except the parallel
postulate. These geometries showed not only the parallel postulate must
be assumed in order to obtain Euclidean geometry but, more important,
that non-Euclidean geometries as mathematical abstractions can and do
exist.
Consider the two-dimensional surface of a sphere, itself embedded in
the three-dimensional space geometry of everyday existence. Euclid s
system accurately describes the geometry of ordinary three-dimensional
space, but not the geometry on the surface of a sphere. Let us consider
two lines locally parallel on the surface of a sphere. They propagate
on the surface as straight as any lines could possibly be, they bend in
their courses one whit neither to left or right. Yet they meet and
cross. Clearly, geodesic lines (on a surface, a geodesic is the
shortest line between two nearby points) on the curved surface of a
sphere do not obey Euclid's parallel postulate.
The thoughts of the great mathematician Karl Friedrich Gauss about
curvature stemmed not from theoretical spheres drawn on paper but from
concrete, down-to-Earth measurements. Commissioned by the government in
1827 to make a survey map of the region for miles around Göttingen, he
found that the sum of the angles in his largest survey triangle was
different from 180. The deviation from 180 observed by Gauss--almost 15
seconds of arc--was both inescapable evidence for and a measure of the
curvature of the surface of Earth.
To recognize that straight and initially parallel lines on the surface
of a sphere can meet was the first step in exploring the idea of a
curved space. Second came the discovery of Gauss that we do not need to
consider a sphere or other two-dimensional surface to be embedded in a
three-dimensional space to define its geometry. It is enough to
consider measurements made entirely within that two-dimensional
geometry, such as, would be made by an ant forever restricted to live
on that surface. The ant would know that the surface is curved by
measuring that the sum of the internal angles of a large triangle
differs from 180, or by measuring that the ratio between a large
circumference and its radius R differs from 2 pi.
Gauss did not limit himself to thinking of a curved two-dimensional
surface floating in a flat three-dimensional universe. In an 1824
letter to Ferdinand Karl Schweikart, he dared to conceive that space
itself is curved: "Indeed I have therefore from time to time in jest
expressed the desire that Euclidean geometry would not be correct." He
also wrote: "Although geometers have given much attention to general
investigations of curved surfaces and their results cover a significant
portion of the domain of higher geometry, this subject is still so far
from being exhausted, that it can well be said that, up to this time,
but a small portion of an exceedingly fruitful field has been
cultivated" (Royal Society of Göttingen, 8 October 1827). The
inspiration of these thoughts, dreams, and hopes passed from Gauss to
his student, Bernhard Riemann.
Bernhard Riemann went on to generalize the ideas of Gauss so that they
could be used to describe curved spaces of three or more dimensions.
Gauss had found that the curvature in the neighborhood of a given point
of a specified two-dimensional space geometry is given by a single
number: the Gaussian curvature. Riemann found that six numbers are
needed to describe the curvature of a three-dimensional space at a
given point, and that 20 numbers at each point are required for a
four-dimensional geometry: the 20 independent components of the
so-called Riemann curvature tensor.
In a famous lecture he gave 10 June 1854, entitled On the Hypothesis
That Lie at the Foundations of Geometry, Riemann emphasized that the
truth about space is to be discovered not from perusal of the
2000-year-old books of Euclid but from physical experience. He pointed
out that space could be highly irregular at very small distances and
yet appear smooth at everyday distances. At very great distances, he
also noted, large-scale curvature of space might show up, perhaps even
bending the universe into a closed system like a gigantic ball. He
wrote: "Space [in the large] if one ascribes to it a constant
curvature, is necessarily finite, provided only that this curvature has
a positive value, however small.... It is quite conceivable that the
geometry of space in the very small does not satisfy the axioms of
[Euclidean] geometry.... The curvature in the three directions can have
arbitrary values if only the entire curvature for every sizable region
of space does not differ greatly from zero.... The properties which
distinguish space from other conceivable triply-extended magnitudes are
only to be deduced from experience."
But as Einstein was later to remark, "Physicists were still far removed
from such a way of thinking: space was still, for them, a rigid,
homogeneous something, susceptible of no change or conditions". Only
the genius of Riemann, solitary and uncomprehended, had already won its
way by the middle of the last century to a new conception of space, in
which space was deprived of its rigidity, and in which its power to
take part in physical events was recognized as possible."
Even as the 39-year-old Riemann lay dying of tuberculosis at Selasca on
Lake Maggiore in the summer of 1866, having already achieved his great
mathematical description of space curvature, he was working on a
unified description of electromagnetism and gravitation. Why then did
he not, half a century before Einstein, arrive at a geometric account
of gravity? No obstacle in his way was greater than this: he thought
only of space and the curvature of space, whereas Einstein discovered
that he had to deal with spacetime and the spacetime curvature.
Einstein could not thank Riemann, who ought to have been still alive. A
letter of warm thanks he did, however, write to Mach. In it he
explained how mass there does indeed influence inertia here, through
its influence on the enveloping spacetime geometry. Einstein's
geometrodynamics had transmuted Mach's bit of philosophy into a bit of
physics, susceptible to calculation, prediction, and test.
Let us bring out the main idea in what we may call poor man's language.
Inertia here, in the sense of local inertial frames, that is the grip
of spacetime here on mass here, is fully defined by the geometry, the
curvature, the structure of spacetime here. The geometry here, however,
has to fit smoothly to the geometry of the immediate surroundings;
those domains, onto their surroundings; and so on, all the way around
the great curve of space. Moreover, the geometry in each local region
responds in its curvature to the mass in that region. Therefore every
bit of momentum-energy, wherever located, makes its influence felt on
the geometry of space throughout the whole universe--and felt, thus, on
inertia right here.
The bumpy surface of a potato is easy to picture. It is the
two-dimensional analogue of a bumpy three-sphere, the space geometry of
a universe loaded irregularly here and there with concentrations and
distributions of momentum-energy. If the spacetime has a Cauchy
surface, that three-geometry once known--mathematical solutions as it
is of the so-called initial-value problem of geometrodynamics--the
future evolution of that geometry follows straightforwardly and
deterministically.
In other words, inertia (local inertial frames) everywhere and at all
times is totally fixed, specified, determined, by the initial
distribution of momentum-energy, of mass and mass-in-motion. The
mathematics cries out with all the force at its command that mass there
does determine inertia here.
One exciting experiment to be performed by the turn of the century will
be the measurement of frame-dragging by the Earth as it rotates. It is
estimated that the gravitational effect of the rotating Earth on the
local spacetime nearby is a measurable effect [330 milliarcsec per
year]. The mass of the Earth has about 0.698 billionth total voting
power as the rest of the universe on our local spacetime!
Homework Problems
Note the answers to the odd (Conceptual Questions, Problems and
Figure-Based Questions) are in the back of your textbook. It is
strongly suggested that you do some of those in every chapter so you
have immediate feedback as how well you are understanding the material.
There are online multiple choice quizzes for each chapter of your
textbook. Goto http://www.mhhe.com/fix then click on
Your book
Student Edition
Choose a chapter
Multiple Choice Quiz
You are expected to do all of your own homework. Statistical patterns
showing copying or collaboration will result in no credit for the
homework assignment for all participants involved. The Code of Academic
Conduct for Iowa Valley Community College District is found in the
Student Handbook.
Physical Science classes require the use of mathematics. If you don't
know algebra, you sould NOT be taking this class. If you need to review,
look at Introduction to Algebra
http://www.math.armstrong.edu/MathTutorial/
WolframAlpha is way faster than a scientific calculator.
http://www.wolframalpha.com
There is little excuse for turning homework in late. You have a whole
week between classes to read the chapters and do the homework. Homework
one week late - half credit. Two or more weeks late - no credit. Do the
homework during the week, not in class! You got homework questions,
email me 24/7. sam.wormley@gmail.com Even if you don't have a homework
question, email me anyway!
Problem 1:
Using you starwheel (planisphere), name three constellations that
are circumpolar.
Problem 2:
Suppose a quasar is observed to increase tenfold in brightness in 4
day. Approximately how large could the quasar be?
Problem 3:
How do electrons and the energy they carry get into the lobes of
radio galaxies?
Problem 4:
How have the quasars evolved over the last 10 billion years?
Problem 5:
What evidence do we have that there may be dead quasars in the
centers of normal galaxies today?
Problem 6:
Use Figure 24.3 to find the distance of a galaxy that has a redshift
of z = 1.0.
Problem 7:
Use Figure 24.10 to find the apparent speed of a component of a
quasar that is moving at 90% of the speed of light in a direction that
makes an angle of 20° to the line of sight to the quasar.
Problem 8:
If the general picture of active galaxies presented in Figure 24.23
is correct, what would we call a low-luminosity active galaxy that we
see at a large viewing angle?
Problem 9:
What evidence do we have that there is more dark matter than
luminous matter in the Local Group of galaxies?
Problem 10:
What is the best way to detect extremely hot gas in clusters of
galaxies?
Problem 11:
As I mentioned earlier one of the biggest problems in astronomy is
measuring distances, especially distances between galaxies. The origin
and fate of the universe depends on how well we know the distances of
galaxies. We also need to know how much mass there is, the expansion
rate, the deceleration rate, and similar cosmological parameters.
General Relativity is central to those questions, so I want you to have
some understanding of it. "Please answer me this", as Papa Joe would
say, "What is or are the most important thing(s) you learned in this
astronomy class"?