MCC PHS 142 M01 Astronomy Homework Ch.1-3
Adj Prof Astronomy: Sam Wormley <sam.wormley@gmail.com>
Web: http://edu-observatory.org/eo/mcc.html
Background Material
Because we have two whole weeks till our next class, I want you
read this four part "Conversations with Papa Joe" by Alan Lightman:
Web - http://edu-observatory.org/mcc/student_resources/Papa_Joe_Story/index.html
Textbook - Read Chapters 1-3
Textbook - http://highered.mcgraw-hill.com/sites/0073512184/student_view0/chapter1/
Textbook - http://highered.mcgraw-hill.com/sites/0073512184/student_view0/chapter2/
Textbook - http://highered.mcgraw-hill.com/sites/0073512184/student_view0/chapter3/
(take the Multiple Choice Quiz for for each chapter)
Textbook - Look at Appendicies 2,3,5 and 12
Textbook - Glossary, pg G-1-14, Words like: Azimuth, Meridian, Transit, etc.
Web - http://edu-observatory.org/eo/constellations.html
Web - http://edu-observatory.org/eo/eclipses.html
Web - http://edu-observatory.org/eo/starcharts.html
Web - http://apod.nasa.gov/apod/ap120731.html
Web - http://antwrp.gsfc.nasa.gov/apod/archivepix.html
Motion of the Sky
"The Earth rotates about its polar axis once a day and produces an
apparent motion on the night sky about the celestial poles. In the
Northern Hemisphere the north celestial pole is elevated above the
horizon. Facing away from the elevated celestial pole, an observer sees
the Sun, Moon, planets, and stars rise in the east and set in the west.
They reach their highest altitude as they cross the local meridian.
When the observer turns to face the elevated celestial pole, stars
nearest the pole neither rise nor set. They become circumpolar and
cross the meridian each day once above the pole at their highest
altitude and once below the pole at their lowest altitude. In the
Northern Hemisphere, circumpolar stars appear to rotate about the north
celestial pole counterclockwise. In the Southern Hemisphere the effect
is reversed and they appear to rotate clockwise.
"Superimposed on the diurnal rotation is an annual rotation caused by
the Earth's orbiting the Sun. Since the stars are seen by the naked eye
after sunset, the constellations appear to move from east to west, and
to return to the same position after a year. Relative to the Sun, the
stars rise and set roughly four minutes earlier each day. In the course
of a month, the night sky appears to move two hours in right ascension
to the west. Also because of this orbital motion of the Earth, the
circumpolar stars in the Northern Hemisphere appear to rotate once a
year in a counterclockwise direction around the north celestial pole
and in a clockwise direction about the south celestial pole.
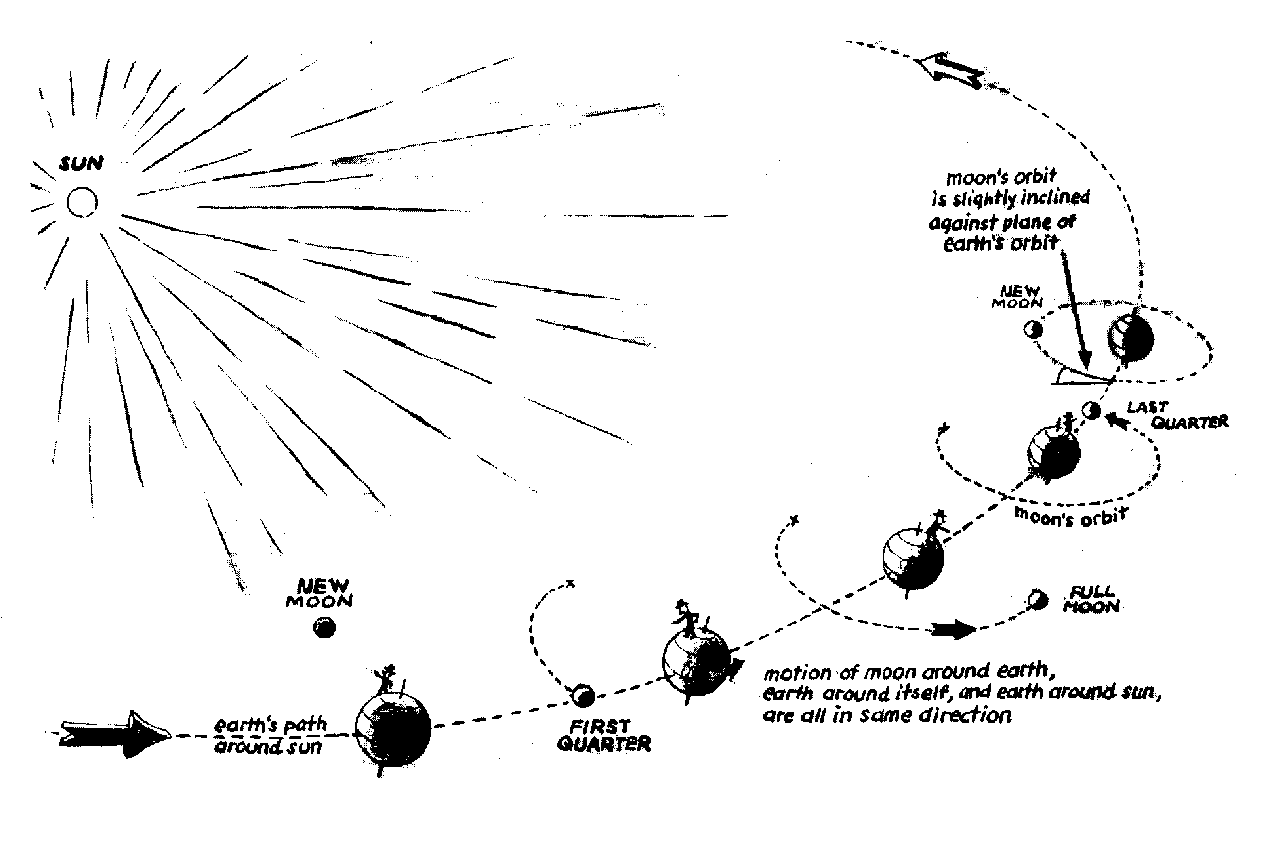
"The Moon moves in an orbit inclined to the ecliptic by 5.1 degrees;
the Moon makes one revolution about the sky from west to east in about
a month. During this period the phases on the Moon complete a cycle
from new to full and back to new. The orbit of the Moon is moving
around the ecliptic, so that other aspects of the Moon's position in
the sky, such as its maximum and minimum declination, change from one
month the next. It is important to know when the planets are in the
most favorable position for observation. The outer planets, for
example, are best seen around opposition. They are in their least
favorable position around conjunction.
"The inner planets are different--they are in their most favorable
position near greatest elongation, even though they are not at full
phase. At superior conjunction the phase is around full, but the
planets are difficult to see because they are further from Earth and
usually too close to the Sun. At inferior conjunction the inner planets
are nearest to the Earth, but again they are difficult to see because
their phase is small, and they are too close to the Sun.
"Often the times of phenomena need not have any great precision;
sometimes the nearest hour, day, or even the nearest week are
sufficient for observational purposes. The dates and times, however,
usually depend on the coordinate system. For historical reasons the
conjunctions and oppositions of planets have always been calculated in
geocentric ecliptic coordinates. On the other hand, the conjunctions of
planets with other planets, bright stars, or the Moon have always been
calculated using equatorial coordinates; the phenomena are then
observed more easily with an equatorially mounted telescope. In some
cases the times of phenomena have been defined as the maxima or minima
of the distances from the Sun or the Earth or the elongation from
another body. In such cases, the phenomena are independent of the
coordinate system".
---From the Explanatory Supplement To The Astronomical Almanac (1992)
Coordinate Systems
There are at least five coordinate systems used in astronomy. We will
concern our selves with three of them.
Geodetic - First consider geodetic coordinates. "Geo" refers
to the Earth. The most common geodetic coordinates used all over the
world are Latitude and Longitude. The MCC campus has geodetic
coordinates very close to 42° North Latitude and 93° West Longitude.
This means that MCC is located 42° north of the Earth's equator and
that it is located 93° west of the "Prime Meridian", that great
circle that passes through Greenwich England and both the north and
south poles. Remember it is 360° all the way around the Earth. See
Figure 1.7 on page 7 of your textbook--substituting "MCC" for
"Riverside Observatory"
Horizon (Horizonal) - Horizonal coordinates consist of an
azimuthal angle (like a magnetic compass) and an altitude, an angle
from the horizon up to an object in the sky. See Figure 1.14 on page
10 of your textbook. When you face north, you are looking in the 0°
direction, east 90°, and so on. What is the azimuth when you are
facing south-west? Every object from your perspective has a unique
pair of horizonal coordinates. An hour later the same object will
have a different set of horizonal coordinates because the Earth (and
you) are turning eastward underneath the sky.
Equatorial - Like the state map of Iowa and country maps with
Latitude and Longitude coordinates, sky charts have a similar grid
system called equatorial coordinates based on the Earth's equator and
poles. The coordinate that corresponds to the north and south of
latitude is call Declination (Dec). Declination is zero at the
celestial equator and is positive up to +90° toward the north and
down to -90° toward the south. In stead of longitude starting at the
prime meridian going through Greenwich England, the left-right scale
is called Right Ascension going from 0-24 hours (this is the same as
going from 0-360°) starting at a point in the sky called the Vernal
Equinox which is where the Sun appears to be in the sky on the first
day of spring. The equatorial coordinate system is essentially fixed
on the stars and the whole coordinate system appears to rotate with
the sky as the Earth (and you) are turning eastward underneath it.
Your Star Wheel (Planisphere)
Your planisphere (star wheel) is a calculator relating all three major
coordinate systems to each other. Planispheres are designed for a
specific latitude and hemisphere on the Earth. Your star wheel is
designed for 42° North Latitude which is exactly right for central
Iowa. Take the time to become familiar with your planisphere.
The circular background chart with stars is printed with equatorial
coordinates of right ascension (in both hours and degrees) and
declination.
o the oval represents all the sky you can see at once
o the center of the oval (zenith) is the point over your head
o the rivet is above the north pole, for us, due north and up 42°
Homework Problems
Note the answers to the odd (Conceptual Questions, Problems and
Figure-Based Questions) are in the back of your textbook. It is
strongly suggested that you do some of those in every chapter so you
have immediate feedback as how well you are understanding the material.
There are online multiple choice quizzes for each chapter of your
textbook. Goto http://www.mhhe.com/fix then click on
Your book
Student Edition
Choose a chapter
Multiple Choice Quiz
You are expected to do all of your own homework. Statistical patterns
showing copying or collaboration will result in no credit for the
homework assignment for all participants involved. The Code of Academic
Conduct for Iowa Valley Community College District is found in the
Student Handbook.
Physical Science classes require the use of mathematics. If you don't
know algebra, you sould NOT be taking this class. If you need to review,
look at Introduction to Algebra
http://dtc.pima.edu/~hacker/primers/algebra-primer/algebra-primer.pdf
http://www.math.armstrong.edu/MathTutorial/
WolframAlpha is way faster than a scientific calculator.
http://www.wolframalpha.com
There is little excuse for turning homework in late. You have a whole
week between classes to read the chapters and do the homework. Homework
one week late - half credit. Two or more weeks late - no credit. Do the
homework during the week, not in class! You got homework questions,
email me 24/7. sam.wormley@gmail.com Even if you don't have a homework
question, email me anyway!
Problem 1:
What time does Sirius (the dog star) transit on the date of your
next birthday? Hint: use your planisphere and placing Sirius on
your local meridian. Important: for me to grade you on this and several
other home work problems, I need you to write your date of birth.
Date of Birth (MM/DD/YYYY): _____________________________
Problem 2:
What time does Aldebaran set on your next birthday? Hint: use
your planisphere, placing Aldebaran on the western horizon, since
Aldebaran is setting in the west.
Problem 3:
What time will Saturn set on your next birthday? Hint: You need
two coordinates to determine a location on your planisphere (star
wheel). Determine the Right Ascension (RA), in degrees, of Saturn from
the table on the back of your planisphere. For Declination note that
many solar system objects, including the major planets, tend to follow
the ecliptic across the sky. The ecliptic is denoted on your
planisphere.
Problem 4:
Hold out your thumb. Beyond your thumb look at an object further away,
such as a chair or tree. While focusing on the more distant object,
notice there are two images of your thumb. Now focus on your thumb and
notice there are two images of the chair or tree in the distance.
That's Parallax.
In astronomy we can do the same thing by looking at a star when the
earth is on one side of its orbit (like the perspective of your right
eye) and then look at the same star six months later when the earth in
on the other side of its orbit (like the perspective of your left eye).
The star will appear to shift with respect to stars (background stars)
much further away.
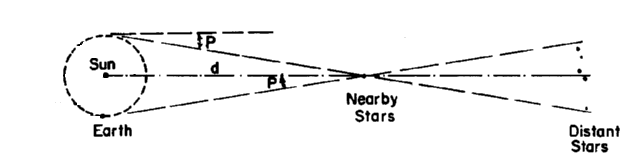Therefore: Parallax(in arcseconds) = 1/Distance(in Parsecs)
Alternatively: Distance(in Parsecs) = 1/Parallax(in arcseconds)
We have measured the parallax angle of over two and a half million
of the nearest stars in our galaxy. I looked up the measured parallax
angle of Barnard's Star, a small red dwarf star, and came up with a
parallax angle of 549.30 milliarc seconds. Google can be really cool
calculator. I used it to find the distance to Barnard's Star in
light-years and got 5.94 light-years.
http://www.google.com/search?q=1%2F.54930+pc+in++light+years
This is even simpler. Since a light-year is defined as the distance
light travels in one year, How long (how much time) does it take
light to reach us from Barnard's Star?
Problem 5:
Set your Planisphere (star wheel) to 11pm on your Birthday. Name a
constellation that is directly over your head. Overhead is in the
center of the oval.
Problem 6:
Using your Planisphere, find and name a constellation that is
circumpolar. Circumpolar means (from out latitude of 42° the
constallation never sets.
Problem 7:
Name a bright star (greater than 2nd or 3rd magnitude that is just
rising at 23h 55m Local Sidereal Time (LST). Hint: LST is the same
at the Right Ascension (RA) of stars on your local meridian. There is
information about magnitude on the back of your Planisphere and on
pages 380-382 of your textbook.
Problem 8:
What is the linear diameter of an object (such as a crater) that has
an angular diameter of 20 seconds of arc (arcseconds) at a distance of
50,000 meters? Show your work and make sure you include all the
right units. Hints: Unless you know trig, use the small angle
formula from your textbook shown on pages 45-46.
Problem 9:
Suppose there is a star which rises at 9pm tonight. At what time did
it rise one month ago? Hint: If you don't know the answer off the
top of your head, you can always use your planisphere to get the right
answer.
Problem 10:
What quantity did Aristarchus have to measure in order to find the
relative distances of the Sun and the Moon?
Problem 11:
In your own words describe something about astronomy that Papa Joe
learned each of the four evenings he visited his great-grandson?